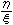4.1.3 数の系 (Ｎ,＋,×) からの比の集合NRの導出
自然数の系 (
,＋,×) からのRの導出を一般化して述べると，以下のようになる。
比の系を導出しようとする数の系（Ｎ,＋,×）では，×が可換であることが条件になる。そしてこのとき，積集合Ｎ*×Ｎの要素の間の同値関係〜が
(ξ,η)〜(ξ′,η′) 
ξ×η′＝ξ′×η
で定義される(註)。Ｎ*×Ｎを〜で類別して得られる類の集合をNRと定義する。
NR の要素ｘに (ξ,η)∈Ｎ*×Ｎが属するとき，ｘを，
| ξ:η， | η/ξ， |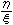 
|
などと表現する。また，ξ：ηを“ξに対するηの比”と呼ぶ。
（註） (ξ1,η1)〜(ξ2,η2) かつ (ξ2,η2)〜(ξ3,η3) のとき，ξ1×η2＝η1×ξ2 かつξ2×η3＝η2×ξ3。
(1) η2∈Ｎ*のとき： ξ2×η2∈Ｎ*。一方，ξ1×η2×ξ2×η3＝η1×ξ2×η2×ξ3，さらに (ξ1×η3)×(ξ2×η2)＝(η1×ξ3)×(ξ2×η2)。したがって，ξ1×η3＝η1×ξ3。
(2) η2＝０ のとき： ξ1×η2＝η1×ξ2 よりη1＝０。また，ξ2×η3＝η2×ξ3 より，η3＝０。よって，ξ1×η3＝η1×ξ3＝０。