8.3 比例関数の表現──“比例定数”
((Ｑ1,＋),(Ｎ,＋,×),×)，((Ｑ2,＋),(Ｎ,＋,×),×) を量の系とし，ｕi をＱi の単位とする（i＝1,2)。
このとき，比例関数ｆ:Ｑ1 ─→ Ｑ2 は，Ｑiの単位ｕi（i＝1,2）に対する関係：
ｆ(ｕ1)＝ｕ2×α
で決まってしまう──実際，
ｆ：ｕ1×ξ 
ｕ2×(ξ×α) (ξ∈Ｎ)
である(註1)。そこで特に，αはｆの表現になる。αの意義は“(Ｑ1の単位ｕ1とＱ2の単位ｕ2に関する)ｆの表現数”であるが，この意義に対する伝統的な言い回しが“比例定数”である。
αがｆの表現であるということを，つぎのように説明することもできる。
関数ｆ：
Ｎ ─→ Ｎ；
ξ ξ×α
に対しつぎの図式が可換となる：
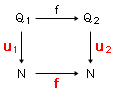
この意味でｆはｆの表現になるが，一方ｆ──α倍の倍関数──に対してはαがこれの表現になる(註2)。
算数科で“一方が２倍,３倍,････になるとき他方も２倍,３倍,････になる関係”──ｆ(ｘ×ξ)＝ｆ(ｘ)×ξ──として指導された“比例関数”が中学校では“ｙ＝ａｘ”に変わってしまうが，比例関数ｆに対するｆが“ｙ＝ａｘ”の正体である。
（註１） ｆ(ｘ)＝ｆ(ｕ1×ξ)＝ｆ(ｕ1)×ξ＝(ｕ2×α)×ξ＝ｕ2×(α×ξ)。
（註２） 先に，量の系に準ずる系として“数空間と同型な系”の概念を導入したが（§6.7.4)，この系の準同型の表現は，（量の系の表現が“比例定数”としての一個の数であったのに対し）数の行列になる。──“線型写像の表現行列”の考え方と同じ。