Up 弧度法，角度の単位「ラジアン」  

    「角度」の意味を言い表そうとすると，うまく言えません。 「角度」の概念・とらえには，ひどく曖昧なところがあるからです。 わたしたちは，《ことばにならないところを無意識に感覚で補って，「角度」の意味をわかったつもりになっている》わけです。

    そこで，数学は，「角度」の意味から曖昧を除くために，「角度」を操作的に定義します。 それが，「弧度法」というものです。

    「弧度法」は，＜円と弧を使って角度を定義する＞アイデアというよりは，＜角度を使わなくて済むようにする＞アイデアです。 「弧度法」の本質は，＜角度を使わなくて済むようにする＞です。


    「弧度法」は，角度を示すのに，１つの円を描き，つぎの絵をつくります：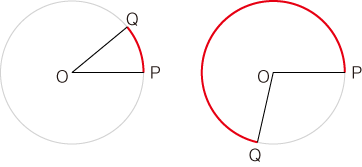
    弧ＰＱの長さで「角度」という量を示唆しているわけです。

    わたしたちの気持としては，つぎの青線で示されるものを「角度」としたいわけですが，この曖昧な青線を退けるところに「弧度法」の意味があるわけです。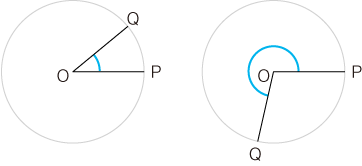

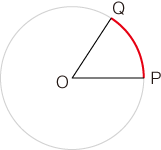
    つぎに，このように導入した量の単位を，弧ＰＱの長さが半径の長さであるものにします：
    そしてこの量を「ラジアン」と名付けます。


    学校数学では，角度の単位として，実用的な「度」と数学的な「ラジアン(radian)」が主題になります。

    度とラジアンの関係は，つぎのようになります：
πラジアン ＝ 180度 (＝ 平角の大きさ)
    （弧ＰＱの長さのπ倍が半円周の長さ。よって，ラジアンのπ倍は平角の大きさ。）