- 直方体の体積は,隣り合う3辺の長さの数値に対する計算で求めることができます。
考え方は,長方形の面積のときと同じです。
<長さの数値が自然数の場合>をやってみましょう。
つぎの直方体の体積 (単位 cm3) を考えます:
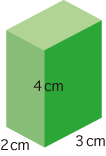
体積を求めるとは,「単位長さ立方の立方体がいくつ入るか」を求めるということです。
そして,単位 cm3 で体積を求めるとは,つぎの詰め込みを考えることです:
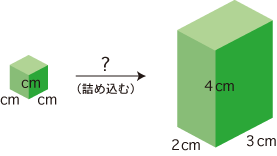
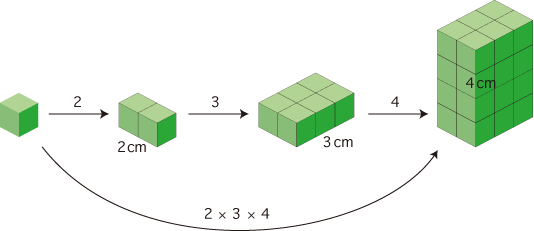
( 確認: 積の意味 (記号「×」の文法)) 確認: 積の意味 (記号「×」の文法))
よって,cm3 を単位とする数値は,2×3×4 になります。
すなわち,
「cm3 を単位とした体積の数値が,
cm を単位としたタテ・ヨコ・タカサの数値の積で求められる。」
ということです。
そして,このことを短く言い表したのが「タテ × ヨコ × タカサ」です。
「タテ × ヨコ × タカサ」は,長さ × 長さ × 長さ ではありません。
「×」は,数に対して定義されます。
「重さ × 重さ × 重さ」を考えよと言われたら,「何それ?!」のリアクションになりますね。「長さ × 長さ × 長さ」にも,このようにリアクションできるようになってください。
- <長さの数値が分数値の場合>にも,みなさんはいま述べた意味の「タテ × ヨコ × タカサ」を既に使っています。
どうしてこの計算になるのか,説明できますか?
つぎの直方体の体積 (単位 cm3) を考えましょう:
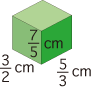
cm 立方の立方体をピッタリ詰め込むことはできません:
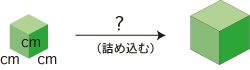
しかし,この直方体の体積は,「cm 立方の立方体の体積の (3/2 × 5/3 × 7/5) 倍」と求められます:
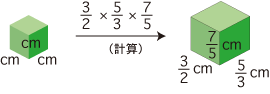 「ヨコとタカサの長さを固定したとき,タテの長さと体積は比例関係にある」
「ヨコとタカサの長さを固定したとき,タテの長さと体積は比例関係にある」
「タテとタカサの長さを固定したとき,ヨコの長さと体積は比例関係にある」
「タテとヨコの長さを固定したとき,タカサの長さと体積は比例関係にある」
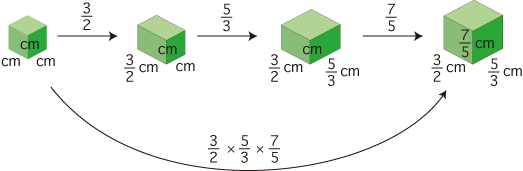
- 「ヨコとタカサの長さを固定したとき,タテの長さと体積は比例関係にある」は,つぎのように説明されます:
- つぎの倍が 3/2 倍になること (上図) を説明します:
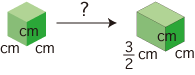
- 左右の直方体のタテの長さを 2 と 3 に共約する長さがとれます。
この長さをタテの長さとし,ヨコとタカサの長さが同じである直方体をとります。これによって,左右の直方体が 2 と 3 に共約されます:
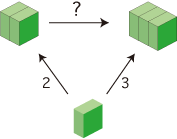
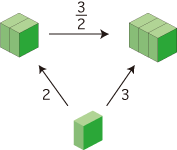
( 確認: 分数の意味) 確認: 分数の意味)
|
 長方形の面積の計算──「タテ×ヨコ」の意味
長方形の面積の計算──「タテ×ヨコ」の意味



 確認: 積の意味 (記号「×」の文法))
確認: 積の意味 (記号「×」の文法))




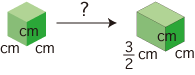


 確認: 分数の意味)
確認: 分数の意味)