また“座標軸”は,n 本の直線(1次元部分空間)   } (i=1,・・・・,n) } (i=1,・・・・,n)
学校数学で教材になる“平面座標”の場合,座標(a,b) の捉え方 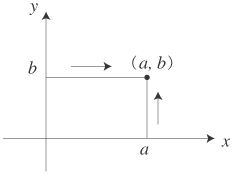
実際,“交点”の解釈を一般化しようとするとき,“直線の交点”ではなく,“超平面の交点”でなければなりません。 ──座標 (α1, ・・・・ ,αn) の点は,n 個の超平面
|
| Up | English | 座標系 |
また“座標軸”は,n 本の直線(1次元部分空間)   } (i=1,・・・・,n) } (i=1,・・・・,n)
学校数学で教材になる“平面座標”の場合,座標(a,b) の捉え方 
実際,“交点”の解釈を一般化しようとするとき,“直線の交点”ではなく,“超平面の交点”でなければなりません。 ──座標 (α1, ・・・・ ,αn) の点は,n 個の超平面
|