\(x\in M\) における方向ベクトルは,
「\(x\) を通る曲線 \(C\) の,\(x\) における方向ベクトル」
として定義される。
| 註: |
「方向」の定義は,「曲線の方向」として定義するのみである。
|
\(C\) を,パラメータ \(t\) を用いて \(C(t)\) と表す:
\[
C : [ -\epsilon, +\epsilon] \longrightarrow M \\
C( 0 ) = x
\]
| 註: |
曲線 \(C\) をパラメータで表すことは,必然である。
\(C\) に関する微分を立てるときは,結局 \(C(t)\) の形を要する。
|
\(C(t)\) の定義には,自由度がある。
これは,同じコースを動く速さの自由度と対応している。
そしてこの「運動」のイメージにしたがうとき,方向ベクトルとは速度ベクトルのことである。
ところで,求めたいのは,「方向」である。
しかし,求めることになるのは「方向ベクトル」である。
なぜ「方向」ではなくて「方向ベクトル」かというと,方向をしめす形は矢印だからである。
矢印の柄の部分をとったら,方向の表示でなくなる。
しかし,速度が違えば異なる長さの柄を与えることになる。
「方向ベクトル」は一意には決まらないもの,というわけである。
| 註: |
一意にする方法は,「正規化」である──大きさが1のものを「方向ベクトル」と決める。
|
以上のことに留意して,以下,「\(x\) を通る曲線の,\(x\) における方向ベクトル」を定義していく。
\(C\) を,\(x\) を通る曲線とする :
\[
C : [ -\epsilon, +\epsilon] \longrightarrow M \\
C( 0 ) = x
\]
\( \phi \) を,「\( x \) を通る \(C\)」が描かれている地図の一つとする :
\[
{\phi}(x) \in {\phi}(C) \subset {\mathbb{R}}^n
\]
また,つぎのようにおく:
\[
{\bf x} = {\phi}(x) \\
{\bf C} = {\phi} \circ C : [ -\epsilon, +\epsilon] \longrightarrow {\mathbb{R}}^n
\]
そして,「\( x \) における \( C\) の方向ベクトル \( {\bf v}_{C,\phi} \)」をつぎのように定義する:
\[
\begin{align*}
{\bf v}_{C,\phi}
&= \frac{d{\bf C}}{dt}(0) = \lim_{{\Delta t} \to 0} \frac{ {\bf C}(0 + \Delta t) - {\bf C}(0)}{\Delta t} \\
&= \lim_{{\Delta t} \to 0} \frac{ {\bf C}(\Delta t) - {\bf C}(0)}{\Delta t}
\end{align*}
\]
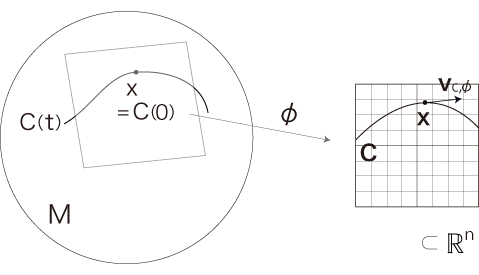
「\( x \) における \( C\) の方向ベクトル」は,地図に依存する:
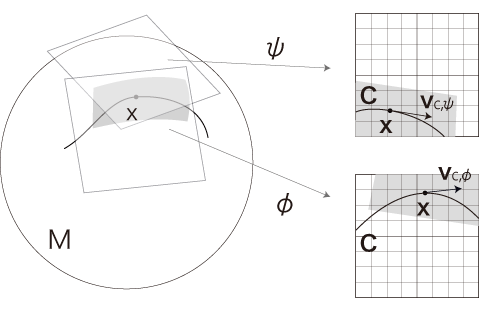
しかし,地図 \( \phi,\, \psi \) の重複部分は,\( C^r \) 級の座標変換 \( \psi \circ \phi^{-1},\, \phi \circ \psi^{-1} \) で対応している。
この座標変換によって,二つの地図の「\( x \) における \( C\) の方向ベクトル」構造は,同型に対応する。
これは,「\( x \) における \( C\) の方向ベクトル」は,一つの地図の上で考えれば十分,ということを意味する。
|

