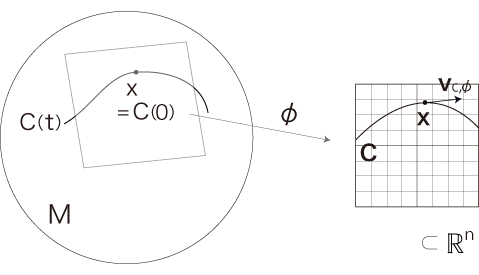
ここで,\(C\) を<\(x\) を通る曲線全体>に亘らせたときの,\( {\bf v}_{C,\phi} \) 全体を考える。 これは,\( \mathbb{R}^n \) の部分ベクトル空間になる。 さらに,このベクトル空間は,\(C^r\) 級座標変換を以て,地図 \(\phi\) によらない。 そこでこれを \(T(x)\) で表し, 「\(M\) の \(x\) における接ベクトル空間」と呼ぶ。 |
| Up | 接ベクトル空間の定義 | 作成: 2018-01-17 更新: 2018-01-17 |

ここで,\(C\) を<\(x\) を通る曲線全体>に亘らせたときの,\( {\bf v}_{C,\phi} \) 全体を考える。 これは,\( \mathbb{R}^n \) の部分ベクトル空間になる。 さらに,このベクトル空間は,\(C^r\) 級座標変換を以て,地図 \(\phi\) によらない。 そこでこれを \(T(x)\) で表し, 「\(M\) の \(x\) における接ベクトル空間」と呼ぶ。 |