地図のデカルト座標を,\(X^i\) 座標と称する。
この基底を,
\[
{\bf E} = \{ {\bf E}_1,\, \cdots,\, {\bf E}_n \}
\]
とする。
曲線座標を,\(x^i\) 座標と呼ぶ。
この基底──局所直線基底──を,
\[
{\bf e} = \{ {\bf e}_1,\, \cdots,\, {\bf e}_n \}
\]
とする
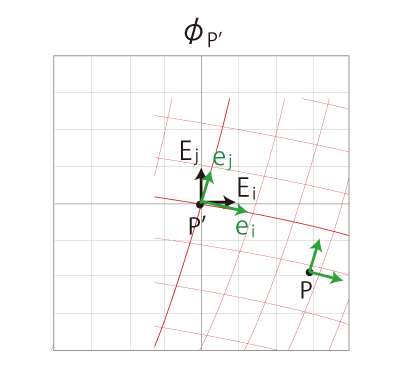
つぎを,この2つの基底の変換式とする:
\[
( {\bf e}_1\, \cdots\, {\bf e}_n )
= ( {\bf E}_1\, \cdots\, {\bf E}_n )
\left(
\begin{array}{ccc}
\kappa^1_1 & \cdots & \kappa^1_n \\
& \cdots & \\
\kappa^n_1 & \cdots & \kappa^n_n \\
\end{array}
\right)
\]
行列 \( (\kappa^i_j) \) は,つぎのように座標の変換行列になる:
\[
\left(
\begin{array}{c}
{X}^1 \\
\vdots \\
{X}^n \\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
\kappa^1_1 & \cdots & \kappa^1_n \\
& \cdots & \\
\kappa^n_1 & \cdots & \kappa^n_n \\
\end{array}
\right)
\left(
\begin{array}{c}
{x}^1 \\
\vdots \\
{x}^n \\
\end{array}
\right)
\]
このとき,
\[
{X}^i = \sum_k \kappa^i_k\, {x}^k
\\ \Longrightarrow
\frac{\partial {X}^i}{\partial {x}^j} = \sum_k \kappa^i_k\, \frac{\partial {x}^k}{\partial {x}^j}
= \sum_k \kappa^i_k\, \delta^k_j
= \kappa^i_j
\]
結局,つぎのようになる:
\[
( {\bf e}_1\, \cdots\, {\bf e}_n )
= ( {\bf E}_1\, \cdots\, {\bf E}_n )
\left(
\begin{array}{ccc}
\frac{\partial {X}^1}{\partial {x}^1} & \cdots & \frac{\partial {X}^1}{\partial {x}^n} \\
& \cdots & \\
\frac{\partial {X}^n}{\partial {x}^1} & \cdots & \frac{\partial {X}^n}{\partial {x}^n} \\
\end{array}
\right)
\\ \\
\left(
\begin{array}{c}
{X}^1 \\
\vdots \\
{X}^n \\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
\frac{\partial {X}^1}{\partial {x}^1} & \cdots & \frac{\partial {X}^1}{\partial {x}^n} \\
& \cdots & \\
\frac{\partial {X}^n}{\partial {x}^1} & \cdots & \frac{\partial {X}^n}{\partial {x}^n} \\
\end{array}
\right)
\left(
\begin{array}{c}
{x}^1 \\
\vdots \\
{x}^n \\
\end{array}
\right)
\]
さらに
\[
( {\bf E}_1\, \cdots\, {\bf E}_n )
=
( {\bf e}_1\, \cdots\, {\bf e}_n )
\left(
\begin{array}{ccc}
\frac{\partial {x}^1}{\partial {X}^1} & \cdots & \frac{\partial {x}^1}{\partial {X}^n} \\
& \cdots & \\
\frac{\partial {x}^n}{\partial {X}^1} & \cdots & \frac{\partial {x}^n}{\partial {X}^n} \\
\end{array}
\right)
\\ \\
\left(
\begin{array}{c}
{x}^1 \\
\vdots \\
{x}^n \\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
\frac{\partial {x}^1}{\partial {X}^1} & \cdots & \frac{\partial {x}^1}{\partial {X}^n} \\
& \cdots & \\
\frac{\partial {x}^n}{\partial {X}^1} & \cdots & \frac{\partial {x}^n}{\partial {X}^n} \\
\end{array}
\right)
\left(
\begin{array}{c}
{X}^1 \\
\vdots \\
{X}^n \\
\end{array}
\right)
\]
つぎを,\({\bf E}\) の基底変換とする:
\[
( {\bf E’}_1\, \cdots\, {\bf E’}_n )
= ( {\bf E}_1\, \cdots\, {\bf E}_n )
\left(
\begin{array}{ccc}
\gamma^1_1 & \cdots & \gamma^1_n \\
& \cdots & \\
\gamma^n_1 & \cdots & \gamma^n_n \\
\end{array}
\right)
\]
基底
\[
{\bf E'} = \{{\bf E’}_1\, \cdots\, {\bf E’}_n \}
\]
に対応する座標を \({X'}^i \) 座標と呼ぶ。
行列 \( (\gamma^i_j) \) は,つぎのように座標の変換行列になる:
\[
\left(
\begin{array}{c}
{X}^1 \\
\vdots \\
{X}^n \\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
\gamma^1_1 & \cdots & \gamma^1_n \\
& \cdots & \\
\gamma^n_1 & \cdots & \gamma^n_n \\
\end{array}
\right)
\left(
\begin{array}{c}
{X'}^1 \\
\vdots \\
{X'}^n \\
\end{array}
\right)
\]
このとき,
\[
{X}^i = \sum_k \gamma^i_k\, {X'}^k
\\ \Longrightarrow
\frac{\partial {X}^i}{\partial {X'}^j} = \sum_k \gamma^i_k\, \frac{\partial {X'}^k}{\partial {X'}^j}
= \sum_k \gamma^i_k\, \delta^k_j
= \gamma^i_j
\]
結局,つぎのようになる:
\[
( {\bf E'}_1\, \cdots\, {\bf E'}_n )
= ( {\bf E}_1\, \cdots\, {\bf E}_n )
\left(
\begin{array}{ccc}
\frac{\partial {X}^1}{\partial {X'}^1} & \cdots & \frac{\partial {X}^1}{\partial {X'}^n} \\
& \cdots & \\
\frac{\partial {X}^n}{\partial {X'}^1} & \cdots & \frac{\partial {X}^n}{\partial {X'}^n} \\
\end{array}
\right)
\\ \\
\left(
\begin{array}{c}
{X}^1 \\
\vdots \\
{X}^n \\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
\frac{\partial {X}^1}{\partial {X'}^1} & \cdots & \frac{\partial {X}^1}{\partial {X'}^n} \\
& \cdots & \\
\frac{\partial {X}^n}{\partial {X'}^1} & \cdots & \frac{\partial {X}^n}{\partial {X'}^n} \\
\end{array}
\right)
\left(
\begin{array}{c}
{X'}^1 \\
\vdots \\
{X'}^n \\
\end{array}
\right)
\]
さらに
\[
( {\bf E}_1\, \cdots\, {\bf E}_n )
=
( {\bf E'}_1\, \cdots\, {\bf E'}_n )
\left(
\begin{array}{ccc}
\frac{\partial {X'}^1}{\partial {X}^1} & \cdots & \frac{\partial {X'}^1}{\partial {X}^n} \\
& \cdots & \\
\frac{\partial {X'}^n}{\partial {X}^1} & \cdots & \frac{\partial {X'}^n}{\partial {X}^n} \\
\end{array}
\right)
\\ \\
\left(
\begin{array}{c}
{X'}^1 \\
\vdots \\
{X'}^n \\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
\frac{\partial {X'}^1}{\partial {X}^1} & \cdots & \frac{\partial {X'}^1}{\partial {X}^n} \\
& \cdots & \\
\frac{\partial {X'}^n}{\partial {X}^1} & \cdots & \frac{\partial {X'}^n}{\partial {X}^n} \\
\end{array}
\right)
\left(
\begin{array}{c}
{X}^1 \\
\vdots \\
{X}^n \\
\end{array}
\right)
\]
曲線座標はデカルト座標に固定されている格好にある。
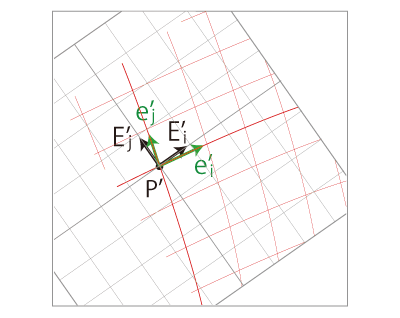
\({X'}^i \) 座標に伴う曲線座標を,\({x'}^i\) 座標と呼び,これの基底──局所直線基底──を,
\[
{\bf e'} = \{{\bf e’}_1\, \cdots\, {\bf e’}_n \}
\]
とする。
よって,
\[
( {\bf e'}_1\, \cdots\, {\bf e'}_n )
= ( {\bf E'}_1\, \cdots\, {\bf E'}_n )
\left(
\begin{array}{ccc}
\frac{\partial {X'}^1}{\partial {x'}^1} & \cdots & \frac{\partial {X'}^1}{\partial {x'}^n} \\
& \cdots & \\
\frac{\partial {X'}^n}{\partial {x'}^1} & \cdots & \frac{\partial {X'}^n}{\partial {x'}^n} \\
\end{array}
\right)
\\ \\
\left(
\begin{array}{c}
{X'}^1 \\
\vdots \\
{X'}^n \\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
\frac{\partial {X'}^1}{\partial {x'}^1} & \cdots & \frac{\partial {X'}^1}{\partial {x'}^n} \\
& \cdots & \\
\frac{\partial {X'}^n}{\partial {x'}^1} & \cdots & \frac{\partial {X'}^n}{\partial {x'}^n} \\
\end{array}
\right)
\left(
\begin{array}{c}
{x'}^1 \\
\vdots \\
{x'}^n \\
\end{array}
\right)
\\ \\
\left(
\begin{array}{c}
{x'}^1 \\
\vdots \\
{x'}^n \\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
\frac{\partial {x'}^1}{\partial {X'}^1} & \cdots & \frac{\partial {x'}^1}{\partial {X'}^n} \\
& \cdots & \\
\frac{\partial {x'}^n}{\partial {X'}^1} & \cdots & \frac{\partial {x'}^n}{\partial {X'}^n} \\
\end{array}
\right)
\left(
\begin{array}{c}
{X'}^1 \\
\vdots \\
{X'}^n \\
\end{array}
\right)
\]
そしてこれより,
\[
( {\bf e'}_1\, \cdots\, {\bf e'}_n )
= ( {\bf E'}_1\, \cdots\, {\bf E'}_n )
\left(
\begin{array}{ccc}
\frac{\partial {X'}^1}{\partial {x'}^1} & \cdots & \frac{\partial {X'}^1}{\partial {x'}^n} \\
& \cdots & \\
\frac{\partial {X'}^n}{\partial {x'}^1} & \cdots & \frac{\partial {X'}^n}{\partial {x'}^n} \\
\end{array}
\right)
\\=
( {\bf E}_1\, \cdots\, {\bf E}_n )
\left(
\begin{array}{ccc}
\frac{\partial {X}^1}{\partial {X'}^1} & \cdots & \frac{\partial {X}^1}{\partial {X'}^n} \\
& \cdots & \\
\frac{\partial {X}^n}{\partial {X'}^1} & \cdots & \frac{\partial {X}^n}{\partial {X'}^n} \\
\end{array}
\right)
\left(
\begin{array}{ccc}
\frac{\partial {X'}^1}{\partial {x'}^1} & \cdots & \frac{\partial {X'}^1}{\partial {x'}^n} \\
& \cdots & \\
\frac{\partial {X'}^n}{\partial {x'}^1} & \cdots & \frac{\partial {X'}^n}{\partial {x'}^n} \\
\end{array}
\right)
\\=
( {\bf e}_1\, \cdots\, {\bf e}_n )
\left(
\begin{array}{ccc}
\frac{\partial {x}^1}{\partial {X}^1} & \cdots & \frac{\partial {x}^1}{\partial {X}^n} \\
& \cdots & \\
\frac{\partial {x}^n}{\partial {X}^1} & \cdots & \frac{\partial {x}^n}{\partial {X}^n} \\
\end{array}
\right)
\left(
\begin{array}{ccc}
\sum_k \frac{\partial {X}^1}{\partial {X'}^k} \frac{\partial {X'}^k}{\partial {x'}^1}
& \cdots &
\sum_k \frac{\partial {X}^1}{\partial {X'}^k} \frac{\partial {X'}^k}{\partial {x'}^n} \\
& \cdots & \\
\sum_k \frac{\partial {X}^n}{\partial {X'}^k} \frac{\partial {X'}^k}{\partial {x'}^1}
& \cdots &
\sum_k \frac{\partial {X}^n}{\partial {X'}^k} \frac{\partial {X'}^k}{\partial {x'}^n} \\
\end{array}
\right)
\\=
( {\bf e}_1\, \cdots\, {\bf e}_n )
\left(
\begin{array}{ccc}
\frac{\partial {x}^1}{\partial {X}^1} & \cdots & \frac{\partial {x}^1}{\partial {X}^n} \\
& \cdots & \\
\frac{\partial {x}^n}{\partial {X}^1} & \cdots & \frac{\partial {x}^n}{\partial {X}^n} \\
\end{array}
\right)
\left(
\begin{array}{ccc}
\frac{\partial {X}^1}{\partial {x'}^1}
& \cdots &
\frac{\partial {X}^1}{\partial {x'}^n} \\
& \cdots & \\
\frac{\partial {X}^n}{\partial {x'}^1}
& \cdots &
\frac{\partial {X}^n}{\partial {x'}^n} \\
\end{array}
\right)
\\=
( {\bf e}_1\, \cdots\, {\bf e}_n )
\left(
\begin{array}{ccc}
\sum_k \frac{\partial {x}^1}{\partial {X}^k} \frac{\partial {X}^k}{\partial {x'}^1}
& \cdots &
\sum_k \frac{\partial {x}^1}{\partial {X}^k} \frac{\partial {X}^k}{\partial {x'}^n} \\
& \cdots & \\
\sum_k \frac{\partial {x}^n}{\partial {X}^k} \frac{\partial {X}^k}{\partial {x'}^1}
& \cdots &
\sum_k \frac{\partial {x}^n}{\partial {X}^k} \frac{\partial {X}^k}{\partial {x'}^n} \\
\end{array}
\right)
\\=
( {\bf e}_1\, \cdots\, {\bf e}_n )
\left(
\begin{array}{ccc}
\frac{\partial {x}^1}{\partial {x'}^1}
& \cdots &
\frac{\partial {x}^1}{\partial {x'}^n} \\
& \cdots & \\
\frac{\partial {x}^n}{\partial {x'}^1}
& \cdots &
\frac{\partial {x}^n}{\partial {x'}^n} \\
\end{array}
\right)
\]
\[
\left(
\begin{array}{c}
{x}^1 \\
\vdots \\
{x}^n \\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
\frac{\partial {x}^1}{\partial {x'}^1}
& \cdots &
\frac{\partial {x}^1}{\partial {x'}^n} \\
& \cdots & \\
\frac{\partial {x}^n}{\partial {x'}^1}
& \cdots &
\frac{\partial {x}^n}{\partial {x'}^n} \\
\end{array}
\right)
\left(
\begin{array}{c}
{x'}^1 \\
\vdots \\
{x'}^n \\
\end{array}
\right)
\]
\[
\left(
\begin{array}{c}
{x'}^1 \\
\vdots \\
{x'}^n \\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
\frac{\partial {x'}^1}{\partial {x}^1}
& \cdots &
\frac{\partial {x'}^1}{\partial {x}^n} \\
& \cdots & \\
\frac{\partial {x'}^n}{\partial {x}^1}
& \cdots &
\frac{\partial {x'}^n}{\partial {x}^n} \\
\end{array}
\right)
\left(
\begin{array}{c}
{x}^1 \\
\vdots \\
{x}^n \\
\end{array}
\right)
\]
|

