リーマン多様体では,各点 \(P\) に対する地図 \(\phi_P\) が所与である。
ふつう,所与性には「任意性」の意味を重ねてしまう。
しかしリーマン多様体の場合は,写像 \(\phi_{P'} \circ {\phi_P}^{-1}\) に対する「\(C^r\) 級」の条件から,地図は,これらの相互関係において,それなりに法則性を現してくることになる。
「リーマン多様体」の学習は,ここで述べる内容の学習が正念場である。
実際,「リーマン多様体」のテクストは,どれもこれも,アブストラクトな表現に終始して,肝心の意味を述べられない。
<わかったつもり><わかったふり>で過ごしている,というわけである。
ここでは,つぎのことを調べる:
「<地図を接ぐ>において,曲線座標の基底はどのよう変化していくか」
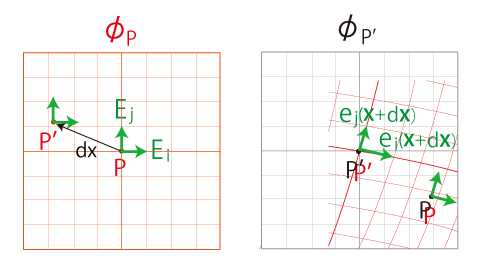
\( \phi_P\) の上で,デカルト座標の基底
\[
{\bf E} = \{ {\bf E}_1,\, \cdots,\, {\bf E}_n \}
\]
を, \( P\) から \( P'\) に平行移動する:
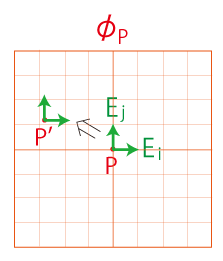
\( \phi_{P'}\) に \( \phi_P\) を読み込む:
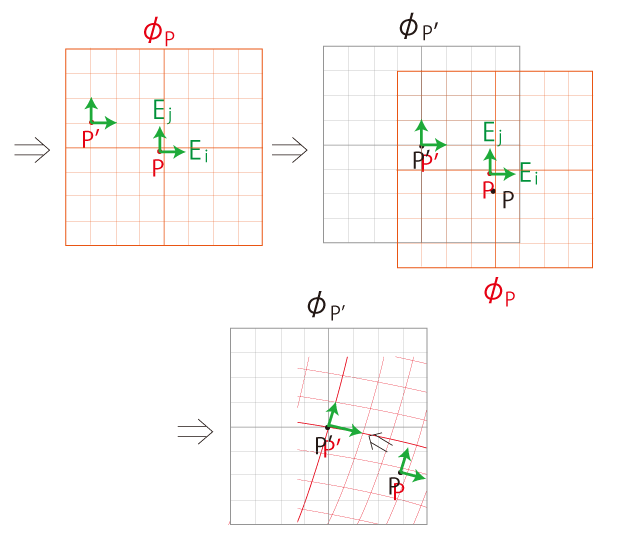
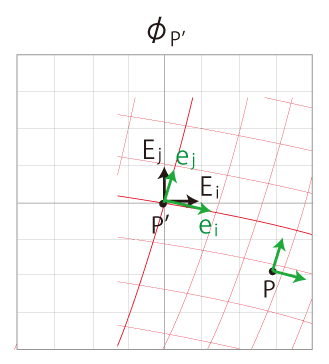
\( {\bf e} = \{ {\bf e}_1,\, \cdots,\, {\bf e}_n \} \) は,曲線座標の基底──局所直線基底──である。
基底 \( {\bf e}\) に対する座標 \(( x_1,\, \cdots,\, x_n )\) と基底 \(\bf E\) に対する座標 \(( X_1,\, \cdots,\, X_n )\) は,つぎの式で変換される
( 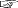 「座標変換」): 「座標変換」):
\[
\left(
\begin{array}{c}
X^1 \\
\vdots \\
X^n \\
\end{array}
\right)
\ =\
\left(
\begin{array}{ccc}
\frac{\partial X^1}{\partial x^1} & \cdots & \frac{\partial X^1}{\partial x^n} \\
& \cdots & \\
\frac{\partial X^n}{\partial x^1} & \cdots & \frac{\partial X^n}{\partial x^n} \\
\end{array}
\right)
\left(
\begin{array}{c}
x^1 \\
\vdots \\
x^n \\
\end{array}
\right)
\\
\left(
\begin{array}{c}
x^1 \\
\vdots \\
x^n \\
\end{array}
\right)
\ =\
\left(
\begin{array}{ccc}
\frac{\partial x^1}{\partial X^1} & \cdots & \frac{\partial x^1}{\partial X^n} \\
& \cdots & \\
\frac{\partial x^n}{\partial X^1} & \cdots & \frac{\partial x^n}{\partial X^n} \\
\end{array}
\right)
\left(
\begin{array}{c}
X^1 \\
\vdots \\
X^n \\
\end{array}
\right)
\]
特に,
\[
\left(
\begin{array}{ccc}
{\bf e}_1 & \cdots & {\bf e}_n \\
\end{array}
\right)
\ =\
\left(
\begin{array}{ccc}
{\bf E}_1 & \cdots & {\bf E}_n \\
\end{array}
\right)
\left(
\begin{array}{ccc}
\frac{\partial X^1}{\partial x^1} & \cdots & \frac{\partial X^1}{\partial x^n} \\
& \cdots & \\
\frac{\partial X^n}{\partial x^1} & \cdots & \frac{\partial X^n}{\partial x^n} \\
\end{array}
\right)
\\
\qquad {\bf e}_i = \sum_j \frac{\partial X^j}{\partial x^i} {\bf E}_j
\\
\left(
\begin{array}{ccc}
{\bf E}_1 & \cdots & {\bf E}_n \\
\end{array}
\right)
\ =\
\left(
\begin{array}{ccc}
{\bf e}_1 & \cdots & {\bf e}_n \\
\end{array}
\right)
\left(
\begin{array}{ccc}
\frac{\partial x^1}{\partial X^1} & \cdots & \frac{\partial x^1}{\partial X^n} \\
& \cdots & \\
\frac{\partial x^n}{\partial X^1} & \cdots & \frac{\partial x^n}{\partial X^n} \\
\end{array}
\right)
\\
\qquad {\bf E}_i = \sum_j \frac{\partial x^j}{\partial X^i} {\bf e}_j
\]
である。
いま,\(\phi_P\) 上の基底 \(\bf E\) の平行移動 \(P \to P'\) を,
\[
{\bf x} \to {\bf x} + d{\bf x}
\]
と見ることにより,\(\phi_{P'}\) の曲線座標の基底 \(\bf e\) を
\[
{\bf e}({\bf x}+ d{\bf x}) = \{ {\bf e}_1({\bf x}+ d{\bf x}), \cdots, {\bf e}_n({\bf x}+ d{\bf x}) \}
\]
と見る。
以下,\({\bf e}_i({\bf x})\) の微分,即ち
\[
de_i ({\bf x}) = e_i ({\bf x}+ d{\bf x}) - e_i ({\bf x})
\]
を,計算する。
ここで「計算」の意味は,「基底 \( \bf E\) ──デカルト座標の基底──に対する表現に直す」である。
基底 \( \bf E \) に対する \( {\bf e}_i ({\bf x})\),\( d{\bf e}_i ({\bf x})\) の座標を,それぞれ
\[
( e_i^1, \cdots, e_i^n ) \\
( de_i^1, \cdots, de_i^n )
\]
とする。──即ち,
\[
{\bf e}_i ({\bf x}) = e_i^1 \, {\bf E}_1 + \, \cdots\, + e_i^n \, {\bf E}_n \\
d{\bf e}_i ({\bf x}) = de_i^1\, {\bf E}_1 + \, \cdots\, + de_i^n \, {\bf E}_n
\]
このとき,
\[
\begin{align*}
e_i^p &= {\bf e}_i({\bf x}) \cdot {\bf E}_p
\\&= \left( \sum_j \frac{\partial X^j}{\partial x^i} {\bf E}_j \right) \cdot {\bf E}_p
\\&= \sum_j \frac{\partial X^j}{\partial x^i} \left( {\bf E}_j \cdot {\bf E}_p \right)
\\&= \sum_j \frac{\partial X^j}{\partial x^i} \delta_{jp}
\\&= \frac{\partial X^p}{\partial x^i }
\end{align*}
\]
これの微分をとる:
\[
\begin{align*}
de_i^p
&= d\left( \frac{\partial X^p}{\partial x^i } \right)
\\&= \sum_l \frac{\partial}{\partial x^l } \left(\frac{\partial X^p}{\partial x^i } \right)\, dx^l
\\&= \sum_l \frac{\partial^2 X^p}{\partial x^l x^i } \, dx^l
\\&= \sum_l \frac{\partial^2 X^p}{\partial x^l x^i }
\left( \sum_m \frac{\partial x^l}{\partial X^m} dX^m \right)
\\&= \sum_l \sum_m \frac{\partial^2 X^p}{\partial x^l x^i }
\frac{\partial x^l}{\partial X^m} dX^m
\end{align*}
\]
これより,
\[
\begin{align*}
d{\bf e}_i
&= \sum_p de_i^p\ {\bf E_p}
\\&= \sum_p
\left(
\sum_l \sum_m \frac{\partial^2 X^p}{\partial x^l x^i }
\frac{\partial x^l}{\partial X^m} dX^m
\right)
\left(
\sum_j \frac{\partial x^j}{\partial X^p} {\bf e}_j
\right)
\\&= \sum_m \sum_j
\left(
\sum_p \sum_l
\frac{\partial^2 X^p}{\partial x^l x^i }
\frac{\partial x^l}{\partial X^m}
\frac{\partial x^j}{\partial X^p}
\right)
{\bf e}_j \
dX^m
\end{align*}
\]
ここで,
\[
\Gamma^j_{im} =
\sum_p \sum_l
\frac{\partial^2 X^p}{\partial x^l x^i }
\frac{\partial x^l}{\partial X^m}
\frac{\partial x^j}{\partial X^p}
\]
とおいて,つぎをまとめとする:
基底 \( {\bf e}({\bf x}) = \{ {\bf e}_1({\bf x}), \cdots, {\bf e}_n({\bf x})\} \) を,上記のように定める。
このとき,
\[
d{\bf e}_i({\bf x}) = \sum_m \sum_j \Gamma^j_{im} {\bf e}_j({\bf x}) \ dX^m \\
\quad
\Gamma^j_{im} =
\sum_p \sum_l
\frac{\partial^2 X^p}{\partial x^l x^i }
\frac{\partial x^l}{\partial X^m}
\frac{\partial x^j}{\partial X^p}
\]
|
|



 「座標変換」):
「座標変換」):
