地図は,地面を舐めるように接がれるわけである。 そしてその地面は,起伏のある地面として考慮されている。 地面の起伏は,\(M\) の情報である。 この情報が,地図に反映される。 この情報連携は,どんな構造になっているのか。 それは,つぎの構造になっている: 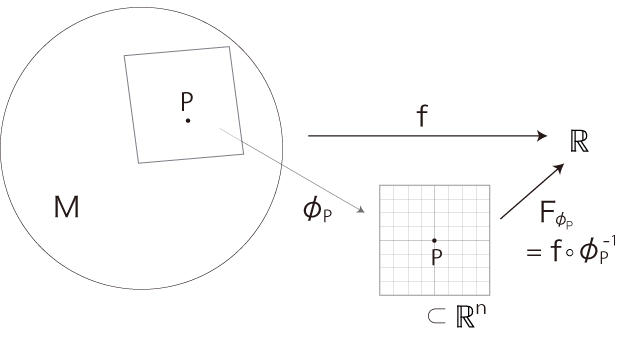
\(f\) は,\(M\) の点にそれの標高を対応させる関数である。 地図 \(\phi_P\) 上の \( {\bf x} = \phi_P(x)\) には,\(F_{\phi_P}\) によって \(f(x)\) が対応している。 これは,各地図において,そこに描かれているすべての点に標高が付されているということである。 地図の特徴的な記号のなかに「等高線」があるが,例えば \( F_{\phi}^{-1}(5) \) は「標高5」の等高線である。 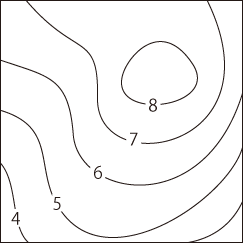
|