「多様体」の話は,地図の話である。 これは,場所場所で地図を好き勝手につくるという話ではない。 地図は,同じ規準でつくられる。 場所場所で正確につくるのである。 しかし,地図は中心から離れたところが実際に対して歪んでくる。 この歪みを計量的に理解しようというのが,「多様体」の話である。 実際,「歪み」は,「<同じ規準>でつくったものの間の相対性」として考えられるものである。 場所場所で好き勝手に地図をつくっていたら,「歪み──相対性」の論にはならない。 多様体でつくる地図は,同じ規準でつくるものである。 その規準は,端的に,「正規直交座標」である。 実際,「歪み──相対性」をこれから主題化しようというとき,なぜ<規準>をわざわざ弛める必要があるか。 「歪み──相対性」を導出できるためには,地図作成の規準は厳格でなければならない。 リーマン多様体は,多様体である。 そしてリーマン多様体は,つぎの条件を以て多様体の特殊である:
そして,\(\phi_P \) の内容は, \(P\) の変化に対してなめらかに変化する。 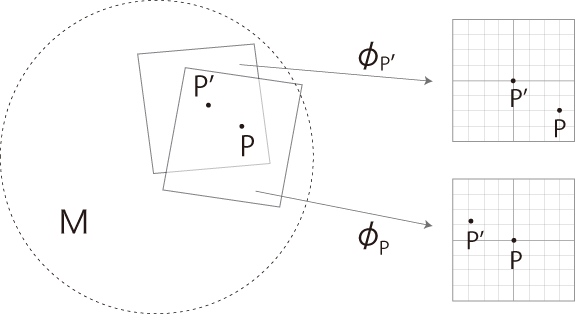
\( M\) の接ベクトル空間の次元 \(n\) に対し,\(\phi_P \subset \mathbb{R}^n\) である。 《どの点も自身の近傍地図をもつ》は,《地図は接いで使う》を含蓄する。 そして《地図は接いで使う》は,《地図は小さい──大きいのは無駄》を含蓄する。 リーマン多様体 \( M\) の地図帳は,そんな地図を束ねたものである。 この「地図帳」は,超越論的な存在になる。 実際,「リーマン多様体」は,超越論である。 |