Up 地図面＝接平面 作成: 2018-01-30
更新: 2018-01-30

    リーマン多様体は，これの各点 \(P\) で，その点中心の地図 \( \phi_P\) をつくる。
    どの地図も，同じ正規直交座標 (デカルト座標) を用いる。
    この意味において，地図は同規格である。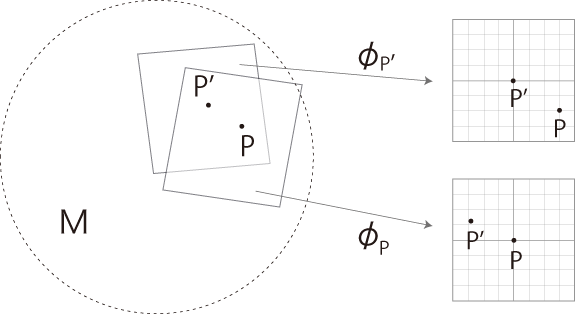


    しかし地図は，規格を定めれば作成に進めるというものではない。
    地図作成では，地面との対面の仕方を考えることになる。
    斜めに対面したら，歪んだ表現になる。
    地図作成では，自ずと一定の「正対」が考えられているわけである。

    リーマン多様体の地図 \( \phi_P\) における「正対」は，「 \(P\) の接平面に置く」である。
    地図 \( \phi_P\) の面は，\(P\) の接平面である。


    「地図」と「接平面」の実体概念を確認しておこう。

    リーマン多様体 \( M \) の次元が \(n\) であるとき，関数
      \[ \begin{align*} \phi : M &\longrightarrow \mathbb{R}^n \\ \qquad P &\longmapsto \phi_P \end{align*} \]
    が「地図帳」であり，\( \phi(P) = \phi_P\) が「地図」である。

    一方，接平面は，\( M \) より高次の空間 \( N \) に \( M \) を埋め込み，\( N \) の部分集合として構築されるものである。
    ──実際，接平面の絵は \( M \) をはみ出すものとして描くわけであるが，このとき暗黙に空間 \( N \) を導入しているわけである。