地図 \(\phi_P'\) に,地図 \(\phi_{P}\) を読み込む。
この結果,曲線座標が導かれる。
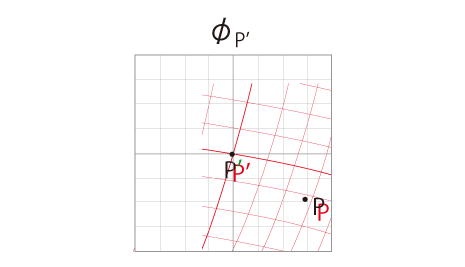
この曲線座標は,いまの自分に対し以前の自分の「真っ直ぐ」を相対化するものである。
「真っ直ぐ」が曲線座標の形で相対化されるようになると,つぎはこの相対性の数量化へと進む。
それは,正規直交座標と曲線座標との間の変換規則──座標変換──を求めることである。
| 註: |
「リーマン多様体」で主題になる「座標変換」は,いま述べたものである。
「直交座標から球面座標への変換」のようなものではない!
|
以下,\(\phi_P'\) 上の座標変換を示す。
| (1) |
\( \phi_P\) のデカルト座標の基底を,
\[
{\bf E} = \{ {\bf E}_1,\, \cdots,\, {\bf E}_n \}
\]
とする。
この基底に対する座標系を,\(X^i\) 座標系と称する。
|
| (2) |
曲線座標 (上図の赤色のメッシュ) を,\(x^i\) 座標系と呼ぶ。
|
| (3) |
\(x^i\) 座標系の基底──局所直線基底──を,
\[
{\bf e} = \{ {\bf e}_1,\, \cdots,\, {\bf e}_n \}
\]
とし,基底 \({\bf E}\) に対する各 \( {\bf e}_i \) の座標を
\[
( e_i^1,\, \cdots,\, e_i^n ) \quad ( i = 1, \cdots, n )
\]
とする──即ち,
\[
{\bf e}_i = e_i^{\ 1} {\bf E}_1 + \cdots + e_i^{\ n} {\bf E}_n \quad ( i = 1, \cdots, n )
\]
|
\(( {\bf E}_1,\, \cdots,\, {\bf E}_n ) \) に対する座標 \(( X^1,\, \cdots,\, X^n ) \) と基底 \(( {\bf e}_1,\, \cdots,\, {\bf e}_n ) \) に対する座標 \(( x^1,\, \cdots,\, x^n ) \) が同じ点を表すとすると,
\[
X^1\,{\bf E}_1 + \cdots + X^n\,{\bf E}_n \\
= x^1\,{\bf e}_1 + \cdots + x^n\,{\bf e}_n \\
= \sum_k x^k \left( \sum_j e_k^{\ j} {\bf E}_j \right)\\
= \sum_j \left( \sum_k e_k^{\ j} x^k \right) {\bf E}_j
\\ \\
\Longrightarrow
X^j = \sum_k e_k^{\ j} x^k \\
\Longrightarrow
\frac{\partial X^j}{\partial x^i} = \sum_k e_k^{\ j} \frac{\partial x^k}{\partial x^i}
= \sum_k e_k^{\ j} \delta^{ki}
= e_i^{\ j}
\]
よって,
\[
(e_i^{\ 1},\, \cdots \, e_i^{\ n} ) = \left( \frac{\partial X^1}{\partial x^i},\, \cdots \, \frac{\partial X^n}{\partial x^i} \right) \\
\ \\
\left(
\begin{array}{c}
X^1 \\
\vdots \\
X^n \\
\end{array}
\right)
\ =\
\left(
\begin{array}{ccc}
\frac{\partial X^1}{\partial x^1} & \cdots & \frac{\partial X^1}{\partial x^n} \\
& \cdots & \\
\frac{\partial X^n}{\partial x^1} & \cdots & \frac{\partial X^n}{\partial x^n} \\
\end{array}
\right)
\left(
\begin{array}{c}
x^1 \\
\vdots \\
x^n \\
\end{array}
\right)
\]
また,後の式から,つぎの式が導かれる:
\[
\left(
\begin{array}{c}
x^1 \\
\vdots \\
x^n \\
\end{array}
\right)
\ =\
\left(
\begin{array}{ccc}
\frac{\partial x^1}{\partial X^1} & \cdots & \frac{\partial x^1}{\partial X^n} \\
& \cdots & \\
\frac{\partial x^n}{\partial X^1} & \cdots & \frac{\partial x^n}{\partial X^n} \\
\end{array}
\right)
\left(
\begin{array}{c}
X^1 \\
\vdots \\
X^n \\
\end{array}
\right)
\]
これが,所期の座標変換である。
|

