しかしここでは,「ベクトル場」と「テンソル場」の間に,「マトリクス場」をはさむことにする。 この構成は,教育的観点から行うものである。 「テンソル」の学習者は,「テンソル」とは何かをわからずに過ごす者である。 こうなるのは,「テンソル」の教授の仕方──それは「テンソル」を「マトリクス」と混同させるだけの教授の仕方──に原因がある。 実際,「マトリクス」を「テンソル」の意味にしているテクストもあるくらいである。 そこで,「テンソル」の前に「マトリクス」を取り上げることで,「テンソルはマトリクスのことではないよ」を示しておこうというのである。 マトリクス (行列) は,線型写像の表現行列のことである。 したがって,「\(f\) 場」の定義図式 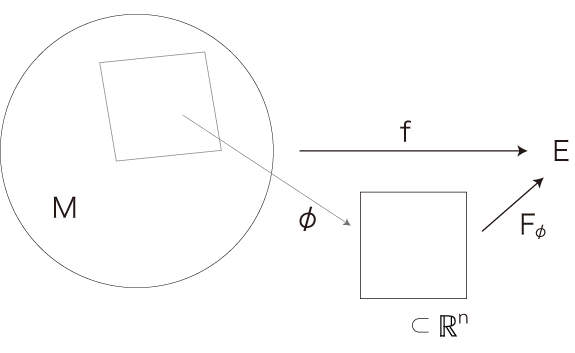
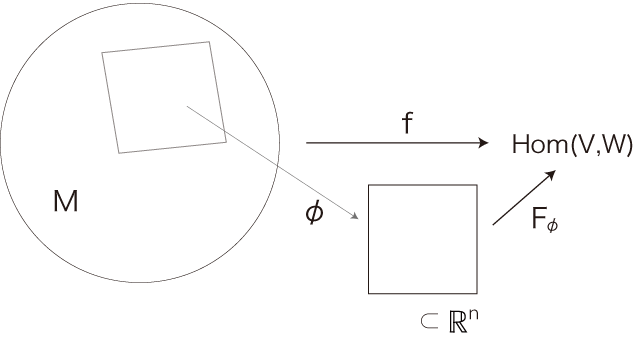
「マトリクス場」とは,どんなふうのものか。 例えば,ある時点での \(M\) の各点 \(x\) の気圧を記述することを考える。 気圧は,空気の単位体積あたり重さで表現できる。 各気圧は \(Hom(体積, 重さ)\) の要素である。 そこで,\(M\) の各点 \(x\) の気圧を記述することは,\(M\) から \(Hom(体積, 重さ)\) への関数fを立てることである。 そして \(M\) は,「\(f\) 場」として,マトリクス場である。 |