Up 曲線座標 作成: 2018-02-17
更新: 2018-02-18

    探査の旅は，＜いま・ここ＞の変化を現すためのものである。
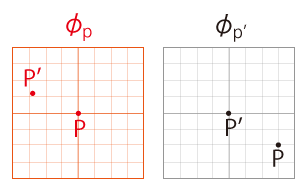
    地図 \(\phi_P'\) は，新しい＜いま・ここ＞である \(\phi_P'\) から，前の＜いま・ここ＞である \(\phi_P\) を，見るためのものである。
    地図 \(\phi_P\) に地図 \(\phi_P'\) を接いだわたしは，\(\phi_P'\) に \(\phi_P\) を書き込むという作業に入る。

      この度の地図作成の目的は，各地の地理を知ろうというのではなく，わたしを空間の中の運動体として現し，反照的に空間の構造・ダイナミクスを現そうとするものである。
      \(\phi_P'\) に \(\phi_P\) を書き込む作業は，わたしを現す作業として行われるものである。

    ＜\(\phi_P'\) に \(\phi_P\) を書き込む＞は，つぎのことをする：
    1. \(\phi_P\) での \(P'\) の座標を \( ({X}_0^i) \) とする。
    1. \(\phi_P'\) 上の点 \( \bf x'\) で，\(\phi_P\) にも載っているものに対し，
        \(\phi_P\) における \( \bf x'\) の座標が \( (X^i)\) であるとき，
        \( ( x'^i ) = ({X}^i - {X}_0^i)\) を \( \bf x'\) の新座標とする。

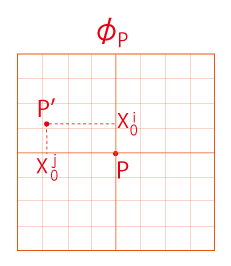
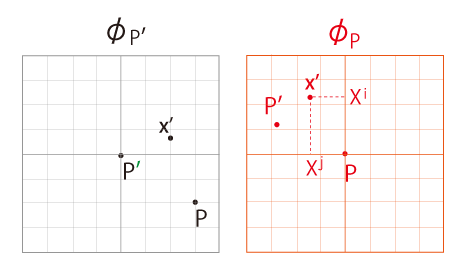
    デカルト座標のメッシュに対応する新座標のメッシュは，下図の赤色のメッシュのようになる：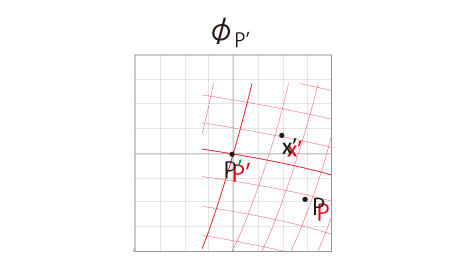

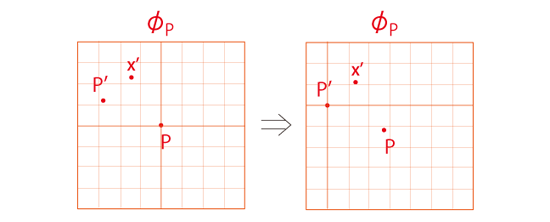
      考え方：
        \(\phi_P\) の原点を \(P'\) に移動
        \(\phi_P' \) に \(\phi_P\) を，原点 (\(P'\)) が一致するように重ね，
        さらに，同じ点が重なるように \(\phi_P\) を変形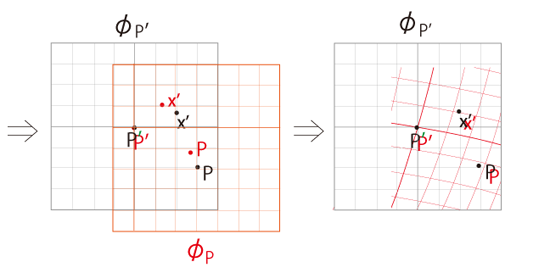

    ここで新座標が曲線座標になるのは，射影のしくみによって，二点間の観測される距離が違ってくるからである。
    ──例えば，\(P,\,P'\) 間の距離の場合だと：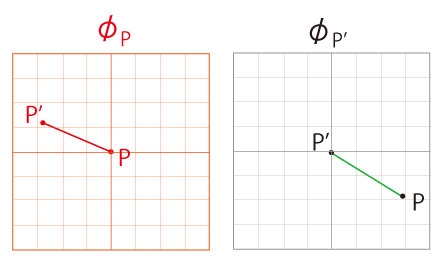

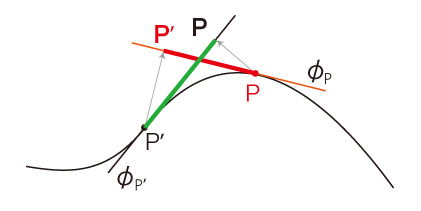
    翻って，曲線座標の解析から，空間の曲がりが知られるようになる。

    「空間探査は空間探査の旅をすることであり，わたしを空間の中の運動体として現すことで，反照的に空間の構造・ダイナミクスを現そうとするものである」というようなことを言ってきたが，それはこういうことである。