下の絵は,接ベクトル空間がもとの空間からはみ出る空間になっている。 接点に立てたデカルト座標の軸は,空間の外側に出ていくのである。 この絵はまた,空間の表面を接ベクトル空間がスライドするような絵になっている。 接ベクトル空間の「シフト」を,「スライド」にしているわけである 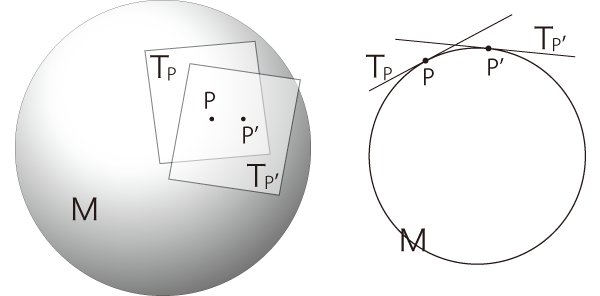
この絵は,3次元へは延長できない。 「3次元への延長」でこの絵を用いるのは,ミス・リーディングということになる。 実際,次元の延長は,単純なものではないのである。 次元の延長は,多様体の絵をすっかり変えるものになる:
要点は,接ベクトル空間 (3次元) のシフトの方向である。 即ち,接ベクトル空間 (3次元) のシフトが進行する軸である。 現実的な軸は,時間軸である。 時間軸を択るとは,空間を「逐次更新する空間」──「進化する空間」──として捉えるということである。 (「一秒前の空間,いまの空間,1秒後の空間」) ──翻って,上の絵で描かれている空間は,「不変な空間」である。 「進化する空間」は,一般次元nで,つぎの絵になる: 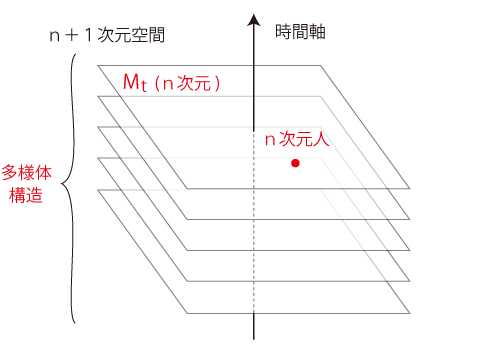
1・2次元の場合だと,つぎのようになる: 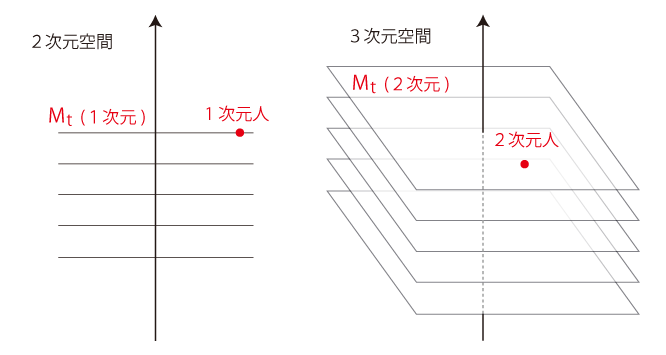
「接ベクトル空間」は,\(M_t\) ごとに考えることになり,かつ「\(M_t\) と重なっていて,不可視」と考える。 \(M\) の点は,\(M_t\) の点として \( (t,\,w ) \ ( w \in M )\) と表記されるものになる。 そして, \( (t,\,w ) \) の近傍 \( U_{t, w} \) と地図 \( \phi_{t, w} \) は,つぎのように描かれるものになる: 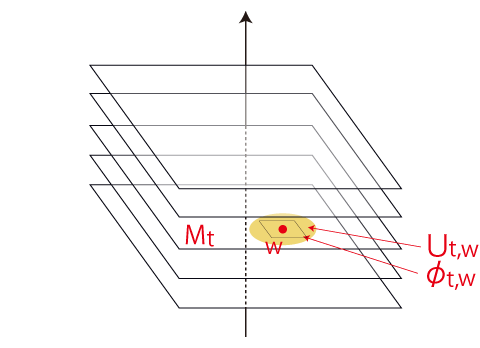
特に,つぎが「地図を接ぐ」の絵である: 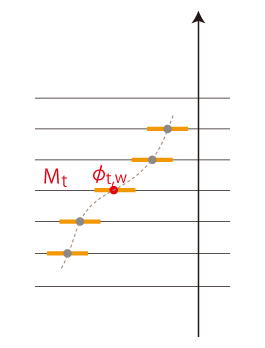
この「地図を接ぐ」は,まったく現実的なものである。 このときの「多様体構造」は,「空間の束」構造である。 「接ベクトル空間」が見えなくなっているが,<地図を書く台>として存在していることになる。 この構造の数学名称は,「ファイバーバンドル」である。 その都度更新される空間を「ファイバー」とする「束 bundle」が,このときの「多様体」である。 |