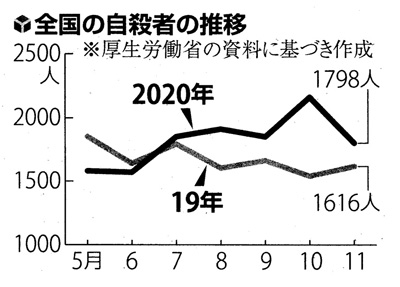
さて，「自殺者数の推移」の度数分布に折れ線グラフを用いるのは，数学的には間違いである。
算数科だと「折れ線グラフの間違った使い方」の題材になる。
「自殺者数の推移」のグラフは，折れ線グラフではなく，棒グラフになる：
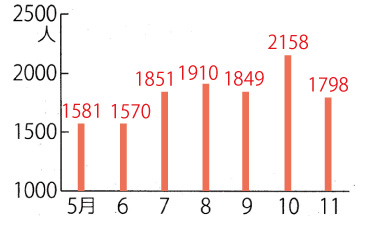
そして，この間の自殺者の総数の計算は，つぎになる：
1581 ＋ 1570 ＋ 1851 ＋ 1910 ＋ 1849 ＋ 2158 ＋ 1798
＝ 12717
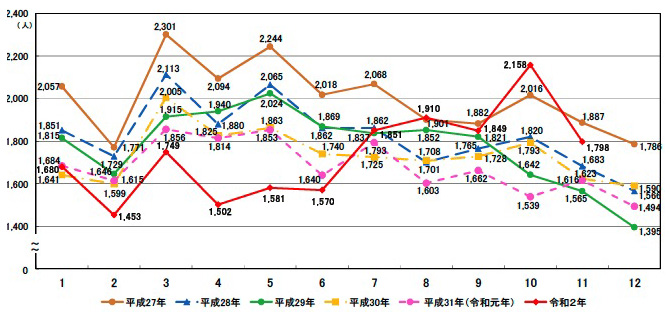
また，前年度のグラフを重ねるときは，つぎのように書くことになる：
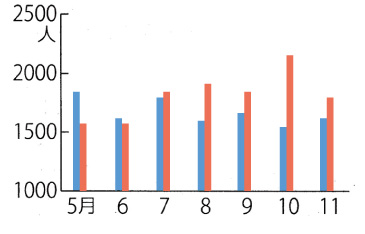
なぜ折れ線グラフはダメなのか。
つぎが，何かの温度変化のグラフだとしよう。
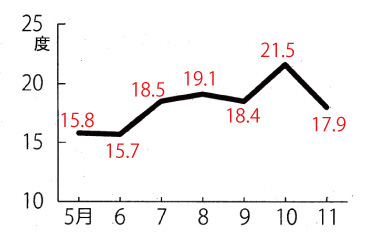
このグラフは，「○月」が「基準時刻から○か月経過した時刻」の解釈になり，そしてその間の「何月何日何時何分何秒‥‥」の温度を概数で読ませることを含んでいる。
これが，折れ線グラフの約束である。
「自殺者数の推移」を折れ線グラフで
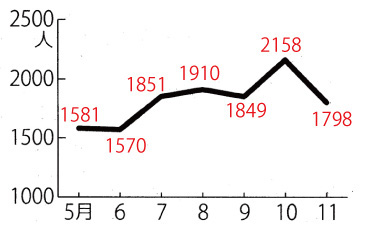
のように書けば，1500人以上の自殺者が切れ目無く発生していることになる。
荒唐無稽である。
ちなみに，縦軸が「人」ではなく「人/単位時間」だと，リアルなグラフではないが，まだしも意味はつく。
時刻ｔの死亡者増加率 (速度) を示すグラフになるわけである。
そして，この間の自殺者の総数の計算ができる。
──例えば「人/月」だと，つぎの計算になる：
\[
\begin{align}
\ \ \ \ & \int_0^{1} \bigl( \frac{ 1570 - 1581 }{ 1 } \,t + 1581\bigr) \,dt \\
& + \int_0^{1} \bigl( \frac{ 1851 - 1570 }{ 1 } \,t + 1570 \bigr) \,dt \\
& + \int_0^{1} \bigl( \frac{ 1910 - 1851 }{ 1 } \,t + 1851 \bigr) \,dt \\
& + \int_0^{1} \bigl( \frac{ 1849 - 1910 }{ 1 } \,t + 1910 \bigr) \,dt \\
& + \int_0^{1} \bigl( \frac{ 2158 - 1849 }{ 1 } \,t + 1849 \bigr) \,dt \\
& + \int_0^{1} \bigl( \frac{ 1798 - 2158 }{ 1 } \,t + 2158 \bigr) \,dt
\\ \\
= \ \ & \frac{ 1570 + 1581 }{ 2 }
+ \frac{ 1851 + 1570 }{ 2 }
+ \frac{ 1910 +1851 }{ 2 } \\
& + \frac{ 1849 + 1910 }{ 2 }
+ \frac{ 2158 + 1849 }{ 2 }
+ \frac{ 1798 + 2158 }{ 2 }
\\ \\
= \ \ & \frac{ 1581 }{ 2 } + 1570 + 1851 + 1910 + 1849 + 2158 + \frac{ 1798 }{ 2 }
\\ \\
= \ \ & 11027.5
\end{align}
\\
\]
 グラフ (度数分布グラフ)
|
