| 「同形」を考える
|
カラダは,対象の同定をする。
カラダが行う「対象の同定」には,タイプ分けが考えられる。
例えば,つぎのように:
- 回転しても,裏返しても,同じ。
- そのうえ,近づけても,遠ざけても,同じ。
- そのうえ,斜めにしても,同じ。
この「対象の同定」を,形を使っていると見よう。
すなわち,「同形」によって「対象の同定」を行っている,と。
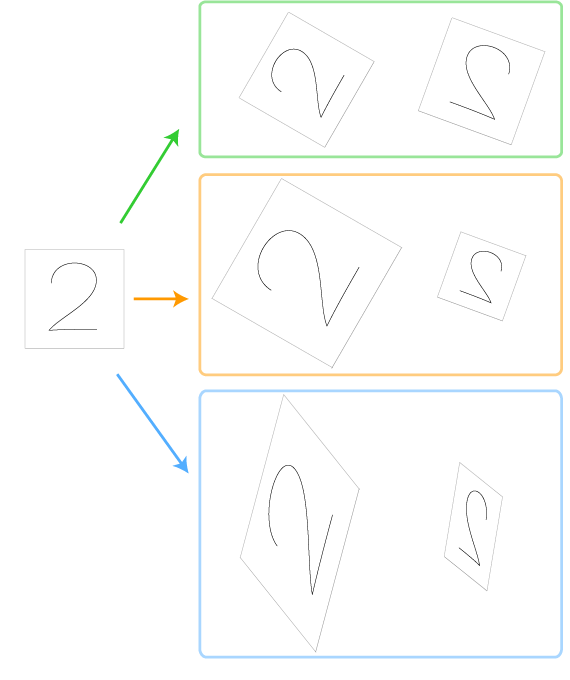
このとき,上の「対象の同定」3タイプには,つぎの「同形」3タイプが対応する:
- 回転しても,裏返しても,同形。
- そのうえ,近づけても,遠ざけても,同形。
- そのうえ,斜めにしても,同形。
|
| 「同形」の数学化
|
この「同形」の数学化を考える。
数学化の方針は:
ヒントは,これ:
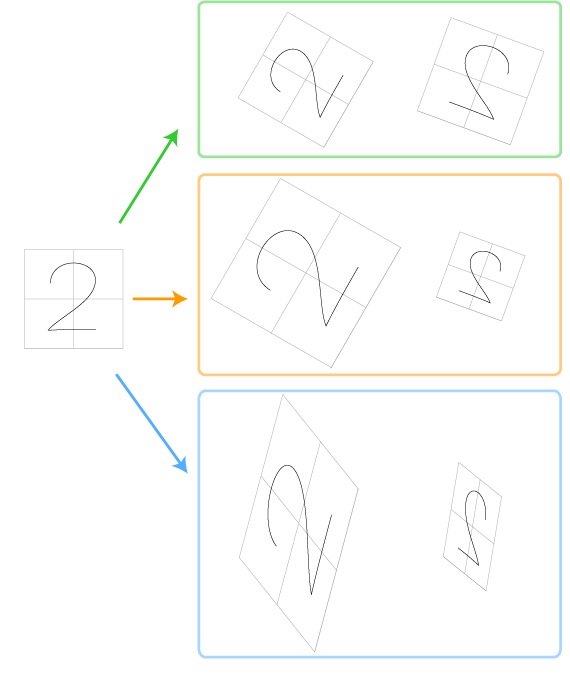
「対応する点=座標が同じ点」が,「同形」の表現になる図形変換ということになる。
上の「同形」3タイプには,つぎの座標枠変換3タイプが対応する:
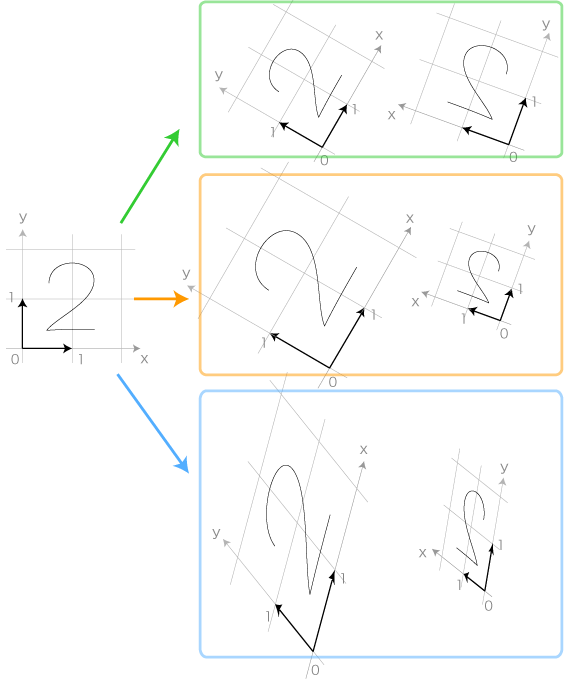
1 は,既習の「合同」。
2 は,既習の「相似」。
3 は,これまで習ったことのないもの。
この 3 の変換は,「線型変換 (1次変換)」と呼ばれる。
なぜこのネーミングなのかは,学習が進む中でわかってくる。
|
| 合同,相似,線型変換の間の含意関係
|
合同は,相似の特別な場合。
相似は,線型変換の特別な場合。
|
座標枠の変換が‥‥ |
| 基底のなす角 |
基底の長さ |
| 合同 |
保存 |
保存 |
| 相似 |
保存 |
一定倍 |
| 線型変換 |
自由 |
自由 |
|
| 収束
|
今日の学習はここまで。
次回の授業では,「線型変換」を,実際に作図してみる。
|
| まとめ
|
今日は,合同,相似の延長となる図形変換が,新しく出てきた。
|