| 「線型変換の計算」を主題化 | 前回は,「線型変換」の作図をした。
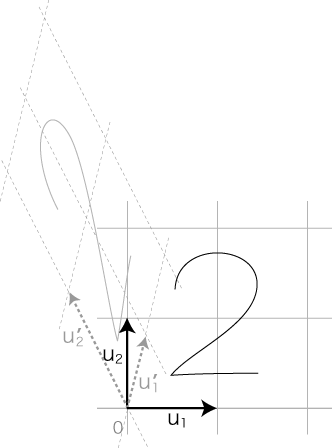 今度は,(x1, x2) に対応する (x'1, x'2) を計算で求められないか,考えてみる。 問題は,つぎの (x'1, x'2) を求めること: u'1 x x1 + u'2 x x2 = u1 x x'1 + u2 x x'2 |
|||
| 計算 | u'1, u'2 を u1, u2 で表せば,これを左辺に代入することで右辺の形の式になる。
そこで,つぎのようにする: u'1 = u1 x a11 + u2 x a12 u'2 = u1 x a21 + u2 x a22 計算すると, x'1 = x1 x a11 + x2 x a21 x'2 = x1 x a12 + x2 x a22 |
|||
| 行列の導入 | (x1, x2) に対応する点の座標計算は,4つの数
 そこで,これらを括って,(x1, x2) の対応先をつぎのように表すことにする: 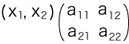 この式の読み方は,
 |
|||
| ベクトルに対する 行列の作用の 計算規則 (アルゴリズム) |
(x1 x a11 + x2 x a21, x1 x a12 + x2 x a22 ) この二つを「=」でつないでみる: 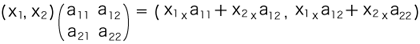 左辺から右辺の式が書けるような規則性が見つからないか? (生徒に見つけさせる) こんな規則になっているわけだ: 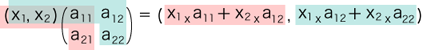 この規則でほんとうに対応先が求まるかどうか,最初の図形で確かめてみよう。 時間の都合から,この点だけやってみよう。 (一つの点を選んで,計算してみせる) |
|||
| 収束 | 今日の学習はここまで。
今日学習したことの練習は,次回の授業でする。 |
|||
| まとめ | 今日は,線型変換の計算を導いた。
計算を考えることで,「行列」が出てきた。 図形の変形は,「行列倍」としてできることになった。 |
| 注意 : | この授業では,つぎの3つの区別を曖昧にしています:
点の座標,点の位置ベクトル,ベクトル 行列の作用はベクトルに対する作用です。 ところが,この授業だと,「座標に対する作用」と誤解されてしまいます。 しかし,点の座標,点の位置ベクトル,ベクトルの区別を正しく行えるには,論理を厳格に運用できる力が必要です。この力は,ここでは生徒に要求できません。(大学の数学の専門課程で鍛える力ということになります。) |