Up 「＜単位の倍＞と＜倍＞の結合」の場合の「かけ算の順序」 作成: 2012-02-22
更新: 2012-02-24

    つぎは，「１あたり量 × いくつ分」の内容が「＜単位の倍＞と＜倍＞の結合」であるときの，これの図式である：
    この図式は，＜単位の倍＞を＜単位＞と＜倍＞に分けるとき，つぎの数学の図式にあと一歩というところに来る：
    翻って，「１あたり量 × いくつ分」は，＜単位の倍＞を＜単位＞と＜倍＞に分けないという一点で，自身を保っているわけである。

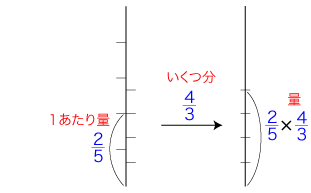
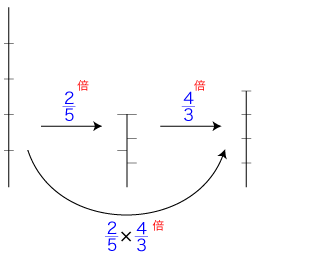
    数の「×」の意味を「１あたり量 × いくつ分」にする立場は，同時に「この順序がかけ算の順序である」と主張する立場である。 そして，「１あたり量 × いくつ分」が「＜単位の倍＞と＜倍＞の結合」であるときは，確かにこの順序の他ではなくなる。 実際，「＜単位の倍＞と＜倍＞の結合」の図式だと，「１あたり量」の前に「いくつ分」をおくことはできない。

    そしてこのときの順序は，数学の「かけ算の順序」と一致する。 しかし，この符合は，単に，数学の「かけ算の順序」を見て「１あたり量 × いくつ分」を発案したためである。
    実際，「１あたり量 × いくつ分」は，自身の系の中で「かけ算の順序」を明証的にすることはできない。 そもそも存在論として自分を立てているからである。