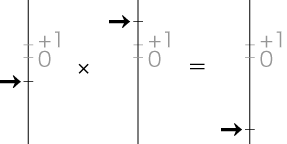学校数学は,<数は量の抽象>である。
特に,数は量である。
自然数は,個数の抽象である。
個数が,自然数を抽象させるところの量である。
そこでつぎが自然数2,3,6である:

ところでこの2,3,6は,2×3=6の関係にある:

翻って,「×」はこの関係の或る読み方を示すものということになる。
さて,どのように読むのか?
つづいて分数。
分数 2/3,4/5,8/15 は,つぎの量である:
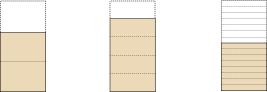
ところでこの 2/3,4/5,8/15は,2/3 × 4/5 = 8/15 の関係にある:
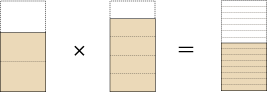
翻って,「×」はこの関係の或る読み方を示すものということになる。
さて,どのように読むのか?
中学数学の「正負の数」は,つぎのように導入される:
| |
《これまで学習した数の数直線で,逆溯行を開始する。》
|
そしてこのときは,数の絵が,これまでの<大きさ>から<位(置)>に変わることになる。
(<数は量の抽象>の立場では,数の絵は<大きさ>の絵になる。しかし,「正負の数」では,強引に<大きさ>の絵をつくることも,ままならない。)
そこで,正負の数 −2,+3,−6は,つぎの位である:
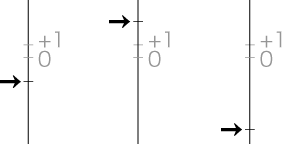
ところでこの −2,+3,−6は,(−2) × (+3) = (−6) の関係にある:
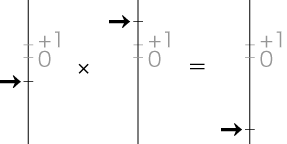
翻って,「×」はこの関係の或る読み方を示すものということになる。
さて,どのように読むのか?
問題になったこれら3つの読み方は,どれもまともにつくることができない。
問題が難しいからではなく,前提にしている<数は量の抽象>がもともと荒唐無稽だからである。
しかし学校数学で「これがかけ算である!」と生徒に指導することになるものは,これである。
| 註 : | ここに教員の苦心・苦労を読むのは,当たっても半分である。
というのも,教員の方も,「これがかけ算である!」を疑っていないからである。
|
さて,「かけ算の順序」の問題は,ここで示した「かけ算」について考えられているのである。
土台が荒唐無稽なところに問題を立てれば,どういうことになるか?
これを見ていくとしよう。
|