Up 逆立式の論理  

    「問題の論理的還元」「積の論理」の概念がないと，立式を「結果オーライであればよいもの」としてやってしまう。 そして，２数の順序を逆転した式を立ててしまう。

    逆立式を合理化しようとすると，ひどくひねくれた論理を作為しなければならない。 この「ひねくれた論理」を，ここで示すことにする。
    複雑だが，＜理解＞にトライされたい。


    記号表記：
    以下の論では，量と数の区別が重要になる。特に，つぎのふたつの区別が重要となる：
    • ２数ｍとｎに関する「ｍとｎの積」
    • 量ｑと数ｎに関する「ｑのｎ倍」

    そこで，この２つの区別がつきやすいように，つぎの表記を用いる：
    • ２数ｍとｎの積を,「ｍ × ｎ」で表す。
    • 量ｑと数ｎに関する「ｑのｎ倍」を,「ｑ × ｎ」で表す。

    また，「２個」「２cm」のように，数と量を直接くっつけた日常表現も以下で使う (式の中では緑色で表す) ので，注意されたい。 ──「２個」「２cm」は，「個 × ２」「cm × ２」と分析されるところのものである。


    先ず，つぎの問題を考える：
      「飴が２個はいった箱があります。３箱のときの飴の個数を求める式は？」


    基本は，これを「２個の３倍」の問題ととらえる。そしてこのとき，

      　 ２個 × ３
      ＝ (個 × ２）× ３
      ＝ 個 ×（２×３）
      ＝ (２×３)個

    となることで，「２×３」の立式となる。
    （最後の「＝」の式変形は，数の「積」の定義そのものである。）

    では，逆立式「３×２」は可能だろうか？
    「３×２」が立式されるとは，最初の問題が「３個の２倍」の問題にとらえられるということである。
    そして，つぎのように考えれば，「３個の２倍」の問題にすることができる：

      各箱から飴１個を取り出す。
      (箱は３個なので）１回につき飴３個が取り出せる。
      (箱の中に飴２個なので) この取り出しは２回行える。
      このとき，飴の個数は，３個の２倍。

    「２×３」と「３×２」の両方が導けたのは，ここでつぎの行列のモデルを使えたことによる：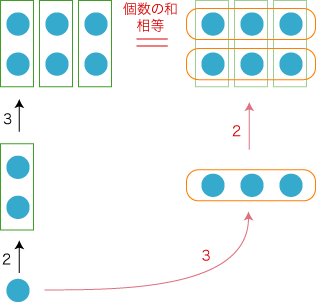




    つぎの問題：
      「2cm のひもがあります。３本つないだ長さを求める式は？」


    基本は，これを「２cm の３倍」の問題ととらえる。そしてこのとき，

      　 ２cm × ３
      ＝ (cm × ２）× ３
      ＝ cm ×（２×３）
      ＝ (２×３)cm

    となることで，「２×３」の立式となる。

    では，逆立式「３×２」は可能か？
    「３×２」が立式されるとは，最初の問題が「３cm の２倍」の問題にとらえられるということである。
    最初の問題を「３cm の２倍」の問題に解釈するには，飴の問題で「飴３個」をつくる工夫をしたときのように，「ひも 3cm」をつくる工夫をしなければならない。 そして，「飴３個」のやり方に倣うことになる：

      各ひもから1cm を切り出す。
      (ひもは３本なので）１回につき合計３cm が切り出される。
      (ひもは最初 3cm なので) この切り出しは２回行える。
      このとき，切り出したひもの合計した長さは，３cm の２倍。

    「２×３」と「３×２」の両方が導けたのは，「行列」に類比のつぎのモデル (ここでは「線分横並びモデル」と呼ぶことにする) が使えたことによる：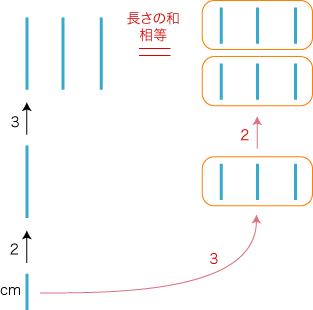




    だんだん解釈が苦しくなる問題にしていく：
      「１秒に２度上昇します。３秒では何度上昇？」


    基本は，これを「２度上昇の３倍」の問題ととらえる。そしてこのとき，

      　 ２度上昇 × ３
      ＝ (度上昇 × ２）× ３
      ＝ 度上昇 ×（２×３）
      ＝ (２×３)度上昇

    となることで，「２×３」の立式となる。

    では，逆立式「３×２」は可能か？
    「３×２」が立式されるとは，最初の問題が「３度上昇の２倍」の問題にとらえられるということである。
    「３度上昇」をつくるのに使えるモデルは，「線分横並びモデル」である：

      各「２度上昇」から「１度上昇」を切り出す。
      (「２度上昇」は３つなので）１回につき合計「３度上昇」が切り出される。
      この切り出しは２回行える。
      このとき，切り出したものの合計は，３度上昇の２倍。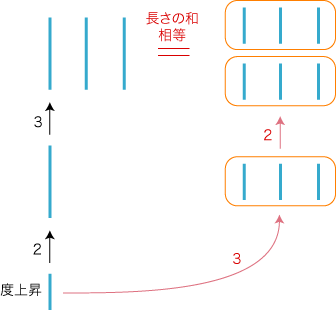


    重要：
    この問題に対する「線分横並びモデル」の適用では，「温度上昇」という量と (視覚表現される)「長さ」という量の数学的同型が，暗黙に用いられている。

    逆立式の解釈 (屁理屈) に，まだあなたがついて来ているとしよう。


    これまでは自然数倍だったが，こんどは有理数倍にする。
    つぎの問題 ：
      「１秒に1.2 度上昇します。3.4 秒では何度上昇？」


    基本は，これを「1.2 度上昇の 3.4 倍」の問題ととらえる。そしてこのとき，

      　 1.2 度上昇 × 3.4
      ＝ (度上昇 × 1.2 ）× 3.4
      ＝ 度上昇 ×（1.2 × 3.4）
      ＝ (1.2 × 3.4)度上昇

    となることで，「1.2 × 3.4」の立式となる。

    では，逆立式「3.4 ×1.2」は可能か？
    「3.4 ×1.2」が立式されるとは，最初の問題が「3.4度上昇の1.2倍」の問題にとらえられるということである。
    「3.4度上昇」をつくるのに，「線分横並びモデル」はもはや使えない。
    線分横並びをくっつけたモデル (「タイルモデル」と呼ぶことにする) にしなければならない：

      「1.2 度上昇の 3.4 倍」を，下図のイメージで考える。
      「度上昇の3.4倍」を，下図のイメージで考える。
      下図のイメージで，「1.2 度上昇の 3.4 倍」は「度上昇の 3.4 倍」の 1.2倍。
      「度上昇の 3.4 倍」は「3.4度上昇」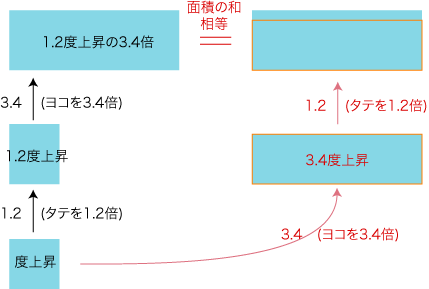




    重要：
    この問題に対する「タイルモデル」の適用では，「温度上昇」という量と (視覚表現される)「面積」という量の数学的同型が，暗黙に用いられている。

    逆立式の解釈 (屁理屈) に，まだあなたがついて来ているとしよう。


    さらに，場面を「空間ベクトルに対する複素数倍」に転じる。
    つぎの問題を考える：
      「単位ベクトルの z 倍として表されるベクトルを，w 倍すると？」


    基本は，これを「単位ベクトルの z 倍の ｗ倍」の問題ととらえる。そしてこのとき，

      　 (単位ベクトル × z ）× ｗ
      ＝ 単位ベクトル ×（z × ｗ）

    となることで，「z × ｗ」の立式となる。

    では，逆立式「ｗ ×ｚ」は可能か？
    タイルモデルは，もはや使えない。
    なぜなら，タイルモデルを使うとは，対象にしている量と (視覚表現される)「面積」の数学的同型を立てるということである。
    上の問題で倍作用として使う数は複素数であるが，「面積」において倍作用として使う数は実数までである。(この意味で，「面積」は実係数。）
    倍作用の数がそもそも異なるという理由で，線分横並びモデル (「長さ」との数学的同型を立てる) も同様に使えない。

    これまで使ってきた「モデル」は，「横断」の操作を行えるようにする視覚モデルであった。 これらのモデルは，複素数を倍作用素とする量に至っては，使えなくなる。


    結論
    1. 量の倍の倍の問題に対し数の積を逆立式するときは，行列モデル，線分横並びモデル，タイルモデルを使うことになる。
    2. これらのモデルの意味は，対象になっている量を２次元の絵に視覚表現 (同型表現) して，その絵の上で「横断」の操作を行うことにある。
    3. 線分横並びモデルの適用では，対象にしている量と (視覚表現される)「長さ」の数学的同型が，暗黙に用いられている。
    4. タイルモデルの適用では，対象にしている量と (視覚表現される)「面積」の数学的同型が，暗黙に用いられている。
    5. 複素数以上になると，適用できる視覚モデル──「横断」の操作をできるようにするモデル──はなくなる。


    数学教育的含意
    1. 逆立式では，行列モデル，線分横並びモデル，タイルモデルが使われる。
      数学的主題の学習目標を (「できる」に対する) 「わかる」に措くとき，逆立式は，モデル適用の論理の理解を伴うものでなければならない。

        論理の理解を伴わない逆立式は，，単に「できる」になる。
        この「できる」は，基本の理解の軽視に進んだり，モデルの誤用という誤りをおかしやすくする。

    2. この意味では，行列モデルの適用による逆立式は，授業内容にすることが可能。
      ──解釈にひねり/難しさがあるので，「発展的」という形の扱いになる。

    3. 一方，線分横並びモデルあるいはタイルモデルの適用による逆立式は，授業内容にできない。
      実際，その解釈もきわめて無理 (作為的) なものになる。 そして，この数学的同型の学習も簡単でない。一般には，大学数学の内容になる。