2で割ったときの余りは,0 (「割り切れる」) か1のいずれかである。 余りを使って自然数を2つに類別できる。 この2つの類に対する名称が,「偶数・奇数」である。 翻って,「偶数・奇数」の授業は,《自然数を,2で割ったときの余りを使って類別》を教える授業である。 この授業につづく授業は,どんなか? 「3だったらどうか?」の授業である。 《自然数を,3で割ったときの余りを使って類別》が主題になり,《自然数は,余り0,1,2の3つの類に分かれる》が内容になる。 そして,この進む先は,つぎの形の一般化である:
──余り0,1,2,‥‥,nー1のn個の類に分かれる》 余りを使った自然数の類別でつくられる類を,「剰余類」と呼ぶ。 すなわち,「nで割ったときの余りを使った類別」に対し,「nを法とする類別」の言い回しを用い,このときの類に対し「nを法とする剰余類」の言い回しを用いる。 このように,「偶数・奇数」の数学は,「剰余類」である。 ちなみに,剰余類を導く数学の方法は,例えば「偶数・奇数」だと,
ここで「m ≡ m′ (mod 2)」の意味は,「mーm′ が2の倍数になる mとm′ は,同類」である。 実際,偶数同士はこの方式で確かに同類となり,奇数同士も同類となる。 一般に,「nで割ったときの余りを使った類別」は「同値関係 mーm′ (mod n) による類別」と同じであり,「nを法とする剰余類」がこのときの剰余類である。 読者は,つぎを「nを法とする類別・剰余類」の絵としてもっているとよい: 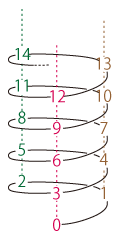
集合論の「同値関係・同値類」で済んでいることがらは,「剰余類」で繰り返さなくてよいわけである。 実際,この「省力」は,「構成主義・系統主義」の立場として数学がまさに大事にしているところのものである。 |