このときの「量表現」は,「もとの量のどれだけ」を形とする。 そして,「どれだけ」をことばにするとき,それが「数」になる。 「どれだけ」は,量の比である。 よって,「数」とは,量の比をことばにしたものである。 「数」として,学校数学では自然数,分数,正負の数,実数,複素数が出てくる。 この「数のいろいろ」は,「量のいろいろ」に応じたものである。 すなわち,対象とする量を単純なものから複雑なものにしていくその都度,量に応じる数を新たにつくることになり,結果として,いろいろな数をもつことになる。 「数」の出自は「量表現」であり,「量の比」が「数」の意味であるから,「数」の主題は基本的に「量の比」に溯るふうになる。 「倍数・約数」の主題は,「量の比」としての「整数比 (分数)」に溯る。 2量の整数比が n/m であるとは,第三の量でこれのm倍,n倍がもとの2量になるものが存在するということである: 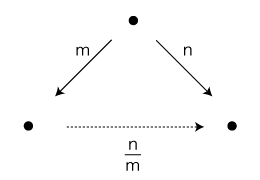
すなわち,同じ比を表現する異なる整数比が無限にある。 実際,整数比 n/m は,任意の自然数kに対し,整数比 (k×n)/(k×m) と同値になる: 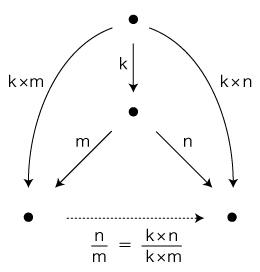
このときの「代表」の考え方は,「最も簡約された表現」である。 そこで,つぎが主題になる: 整数比の簡約は,「2数のそれぞれを積に分解 (因数分解) して,2数を共約する数を見つける」が方法になる。 そこで,つぎが主題になる: 最も簡約された整数比は,2数を共約する数がない場合である。 そこで,つぎが主題になる: 整数比を既約にする (整数比の2数を互いに素にする) 方法は,2数の公約数のうち最大のもので2数を除することである。 (実際,最大公約数pで除した結果の2数が互いに素ではなくてqを公約数にもつとき,p×qが最初の2数の公約数ということになり,pが最大公約数であることに矛盾する。) こうして,つぎが主題になる: 「最大公約数」が主題になると,つぎに最大公約数を求める方法が主題になる。 方法は,「2数それぞれにおいて因数分解をこれ以上はできない形にまで進め,2数に共通の因数積で最大のものを求める──共通の因数積で最大のものが最大公約数になる」である。 こうして,つぎが主題になる: |