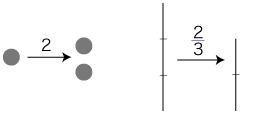
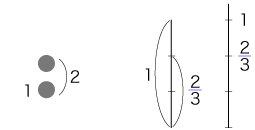「量」がわかるとは，つぎの系としてわかるということである。
この系には，４つの算法がある。 これらは，規則で互いにつながっている。 量計算は，これらの算法の運用である。 したがって，量(系) がわかっていなければ量計算はできないという理屈になる。 しかし，量(系) の理解は，ふつうにできることではない。 そこで，擬似論理でやり過ごすとかノウハウでやり過ごすとかの工夫になる。 算数科の「数と量」は，これをやっていくことになる。 このことに是非はない。 こういうわけで，算数科は，( ( 量(集合), ＋ ), ×, ( 数(集合), ＋, × ) ) の４つの算法のうちから ＋ と × をなくしている (註)。 実際，算数の教科書には，＜量と量の和＞，＜量に対する数の倍＞の式表現はないことになっている。 もし「2cm ＋ 3cm」「2cm × 3」のような式が教科書に載っていたり，教員が授業で使っているとしたら，それは不注意か，知らないことに因るものである。 しかし ＋，× をなくす措置は，教員・生徒が，量計算を数計算に形式感覚で一挙にもっていかねばならないことを意味する。 ＋ の方は，「一挙に」をまだ暗黙にやれる余地がある。 問題は，× の方である。 簡単な量計算ならともかく，少し複雑な量計算になるともう無理である。
「何秒」は，秒の何倍：
「ｂｍ」＝ｍ × ｂ
そこで，算数科はどうしたか？ 数の計算式を導く立式ツールの開発に向かった。 今日，算数科は「倍」「倍の倍」を「二重数直線」で教えるようになっているが，「二重数直線」は立式ツールである。 また，「倍作用」を封じることは「倍」の新たな定立の仕方に向かわせることにもなる。それが「倍は関数」である。 どういうことか？ 数２は，長さ(要素) に対する倍作用素として，つぎの関数を導く：
|
『「数直線でかけ算・わり算」は，わかるのがおかしい』
