例えば,長さ,重さに対する数の倍を分数倍で考えているとき,長さ(系) と重さ(系) は同型である。 長さに対する数の倍を自然数倍で考え,重さに対する数の倍を分数倍で考えているとき,長さ(系) と重さ(系) は同型でない。 量(系) Qの構造が構成要素の数(系) Nによって定まるのは,どのようなしくみによるのか。 数(系) Nの構造を組み替えて,量(系) をつくることができる。 すなわち<量としての数>がつくられる。 そして,Qはこの<量としての数>と同型になっている。 これが,<量としての数>の概要である。 以下,この内容を明示的に述べる。 (1) <量としての数> 数(系) (N, +, ×) を素材にして,
これは,量(系) の構造をもつものになる──すなわち,量(系) になる: (2) <量としての数>は,量の普遍対象 gを,量Qの零でない要素とする。Qの要素と数の対応:
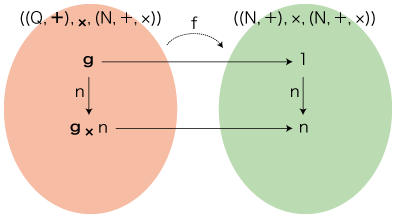
すなわち,( (N, +), ×, (N, +, ×) ) は,Nの要素を倍の作用素として考えるすべての量 ( (Q, +), ×, (N, +, ×) ) にとって,この量の構造を示すものになっている。 このことは,数学の「普遍対象 (universal object)」のことばを用いて,つぎのように表現される:
「普遍対象」は,いわば,イデア論の「イデア」である。 ( (N, +), ×, (N, +, ×) ) は <Nを作用域とする量>のイデアであり,イデア ( (N, +), ×, (N, +, ×) ) の降りてきたものが <Nを作用域とする量>である。 ──実際,数学で自体的に存在するのは,数であって,量ではない。
|
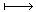 n (n∈ N)
n (n∈ N)
 , +, ×) に対する量 ( (
, +, ×) に対する量 ( (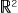 , +), ×, (
, +), ×, (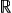 , +, ×) ) は量ではないが,複素数をスカラとしたときの1次元の線型空間 ( (
, +, ×) ) は量ではないが,複素数をスカラとしたときの1次元の線型空間 ( (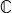 , +, ×) ) は,( (
, +, ×) ) は,( ( 『「数とは何か?」への答え』
『「数とは何か?」への答え』