そしてその理は? 数学教育生態系は,運動する系であり,力学系である。 数学教育生態系の論述は,「数学教育のダイナミクス」の論述である。 「生態学方法論」の章では,「数学教育のダイナミクス」をつぎのようにカテゴリー分けした: 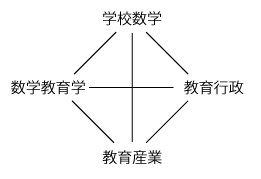
それを中心に据えた「数学教育のダイナミクス」の論考をつくる》 この「学校数学」の章では,学校数学を中心に据えた「数学教育のダイナミクス」を論考する: 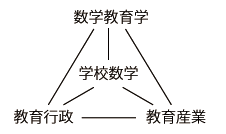
(1) 「数学が必要」 「文明開化」は,「西欧化」である。 「西欧化」は,「殖産興業・富国強兵」をスローガンにする。 「西欧化」の内容の一つに学校教育があり,学校教育の一分野として数学教育 (学校数学) が定まる。 数学教育の理由づけは,「産業の基礎科学のさらに基礎学として数学は必要」である。 (2) 学校数学の生業 学校数学の「経営・企画・制作・営業」の生業がつくられる。 (3) 「一般陶冶」「数学的○○」 併せて,学校教育の規模拡大が随う。──高等教育を受けることが一般化する。 ここに,数学教育に対する「産業の基礎科学のさらに基礎学として数学は必要」の理由づけが,時代と合わなくなる。 数学教育は,「全ての者にとって数学は必要」を存在理由にするものに,変わらねばならなくなる。 こうして,数学教育は「一般陶冶」を立てることになる。 そして出てきたのが,「数学的○○」である。 (4) 「基礎・基本」と「数学的○○」と受験数学 これが学校現場に丸投げされる。 学校現場は「数学的○○」の形づくりに励む。 この結果は,《授業が数学の授業でなくなる》になる。 《授業が数学の授業でなくなる》は,これがこれで済むものなら,教員と生徒の両方にとってありがたいものになる。 実際,数学の教授/学習は,教員,生徒にとって荷が重過ぎるものである。 こうして,「数学的○○」は,数学教育のモジュールとして定着する。 しかし,学校数学は,《授業が数学の授業でなくなる》では済まない。 「産業の基礎科学のさらに基礎学として数学は必要」は,生きている。 教育行政は,この看板を下ろすことはない。 生徒も,《授業が数学の授業でなくなる》に乗るわけにはいかない。 生徒は,将来の生業に向けて競争する存在である。 この競争の内容に,数学の成績がある。 受験数学が数学教育の中で安定した位置を保ち続けている所以である。 《授業が数学の授業でなくなる》のつけを払わねばならないのは,結局生徒である。 実際,現前の「数学教育」はつぎの3つの併存である:
(5) 「自分によかれ」 安定させている力は,「人の生業」である。 一般に,企業は「人によかれ」で運営しているのではない。 「自分によかれ」で運営している。 ただ,企業の成立は,「顧客満足」が条件になる。 こうして,企業は,《「人によかれ」で運営している》の見掛けをもつものになる。 生業になった数学教育は,「生徒によかれ」で運営しているのではない。 数学教育を生業う者の「自分によかれ」で運営している。 (「営利大学」で問題になった授業形態・授業カリキュラムに,このことがよく見てとれる。) ただ,数学教育の成立は,「生徒満足」が条件になる。 こうして,数学教育は,《「生徒によかれ」で運営している》の見掛けをもつものになる。 数学教育を生業う者の心理は,「自分によかれ」を抑圧してこれを見ないようにする。 数学教育を生業う者は,自分は「生徒によかれ」をやっていると思っている。 (6) 疎外論 「数学の教授/学習」の理念形 (普遍形) は,<生活>に入ると,現前の学校数学のようになる。 その<生活>は,いまは特に<商品経済>である。 理念形が現実の形に変わることを,「疎外」と謂う。 「疎外」にネガティブな意味はない。 <現成>は<疎外>である。 実際,商品経済の数学教育の第一義は,商品経済の確かな歯車になっていることである。 現前の「数学教育」は,この役を果たしている。 即ち,<人に生業を与え,経済効果を生み続けているもの>になっている。 「数学的○○」の箱物性も,「経済効果を生み続ける」に適っている。 箱物は埋まることがないから,箱物を埋めようとする営みは延々と続けられる。 現前の「数学教育」は,商品経済の理の実現である。 そして,商品経済の理の実現である故に,現成である。 |