日出/日入時刻は,同じ地点でも,観測点の高度によって違ってくる。
つぎが,違うことを説明する図である:
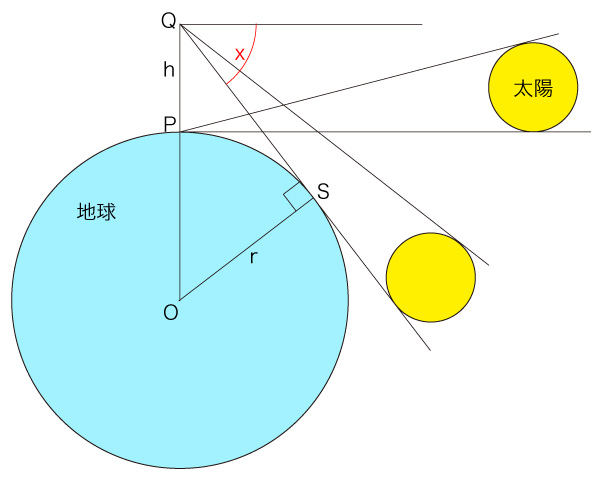
ここで \( P, Q \) は,高度がそれぞれ \( 0, h \) の観測点。
1日を
\( 24 \) 時間 = \( ( 60 \times 60 \times 24 ) \) 秒
とすると,太陽は1度を
\( ( 60 \times 60 \times 24 ) / 360 \) = 240 秒
で移動している。
よって \( x \) ラジアンの移動にかかる時間 \( t \) 秒は,
\[
t = 240 \times \Bigl( \frac{ 180 }{ \pi }\ x \Bigr)
\]
\( x \) は,つぎの関係式から求まる:
\[
sin \Bigl( \frac{ \pi }{ 2 } - x \Bigr) = \frac{ r }{ r + h }
\]
以上まとめて,
\[
t = 240 \times \frac{ 180 }{ \pi }\ \times \Bigl( \frac{ \pi }{ 2 } - sin^{-1} \Bigl( \frac{ r }{ r + h } \Bigr)\Bigr)
\]
地球の半径 \( r \) を
\( 6378 \times 10^3\ \ m \)
として具体的に計算してみると:
| 高度 (m) |
時間差 (秒) |
| 5 |
17.22 |
| 10 |
24.35 |
| 15 |
29.82 |
| 20 |
34.44 |
| 25 |
38.5 |
| 30 |
42.18 |
| 35 |
45.56 |
| 40 |
48.7 |
| 45 |
51.65 |
| 50 |
54.45 |
| 55 |
57.11 |
| 60 |
59.65 |
| 65 |
62.08 |
| 70 |
64.42 |
| 75 |
66.69 |
| 80 |
68.87 |
| 85 |
70.99 |
| 90 |
73.05 |
| 95 |
75.05 |
| 100 |
77 |
|

