「ビッグバン」教に入信すると,「宇宙の年齢」が計算できる。
「宇宙の年齢:13.799±0.021 億年」の類は,これである。
以下,この計算法を示す。
「ビッグバン」説
《すべての天体は,溯れば同じ1点 (「ビッグバン」) である》
に対し,つぎの仮定を加える:
このとき,任意の二天体が互いに遠ざかる速さは,一定である。
よって,ある天体を観測して,それの地球との距離rと地球からの後退速度vが求まるとき,ビッグバン (両者の距離が0の場合) はいまより \( t = \frac{r}{v} \) 前だったことになる。
ここで,「ハッブルの法則」が用いられる:
| |
|
地球から後退する任意の天体において,地球とそれとの距離 \( r \,Mpc \) と地球からの後退速度 \( v \,km/秒 \) の間に, つぎの関係が成り立つ:
\[
v = H_0 \,r \\
H_0 = 72 \ \ \ \left[ \frac{km}{MPC \cdot 秒} \right]
\]
|
|
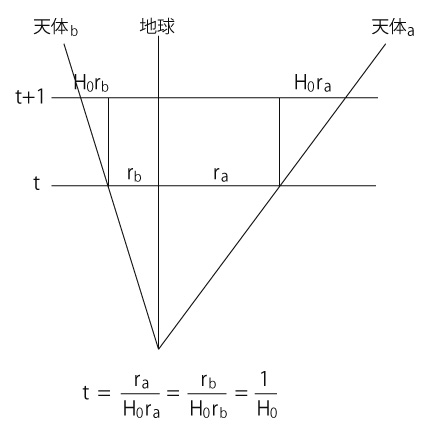
これより,
\[
t = \frac{r}{v} = \frac{1}{H_0} = 0.014 \ \ \ \left[ \frac{MPC \cdot 秒}{km} \right]
\]
ここで,
\[ Mpc = 3.082 × 10^{19} \,km \\
年 = (365 × 24 × 60 × 60) \,秒 = 31536000 \,秒 \\
\ \ \ \ \Rightarrow \ 秒 = 3.17 × 10^{-8} \,年
\]
よって,
\[
0.014 \left[ \frac{MPC \cdot 秒}{km} \right] \\
= 0.014 × (3.082 × 10^{19}) × (3.17 × 10^{-8}) \left[ \frac{km \cdot 年}{km} \right] \\
= 137 × 10^8 \,[年] = 137 \,[億年]
\]
|

