Up 経度余弦方程式の解判定 作成: 2020-09-15
更新: 2020-09-20

    緯度ａの日出/日入/正午点の経度は，公転角度τで決まる。
    この経度を，b(τ) と表すことにする。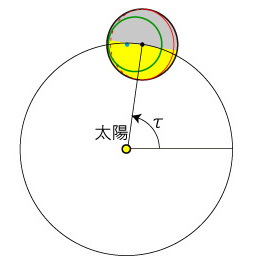


例：正午(夜)の場合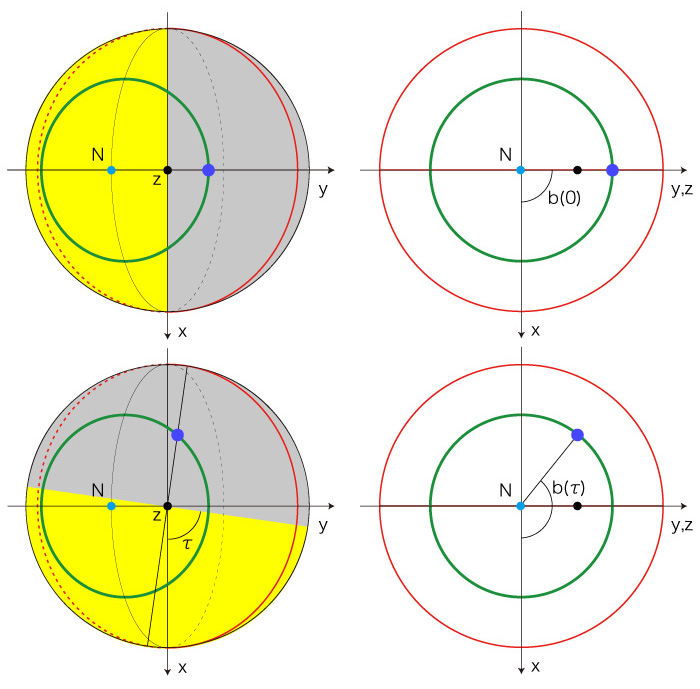

    b(τ) は余弦方程式の解として計算され，解はつぎの３通りになる：
    • cos( b(τ) ) = 1 のとき，b(τ)＝ 0
    • cos( b(τ) ) = -1 のとき，b(τ)＝π
    • cos( b(τ) ) ≠ ±1 のとき，解は2つ：0 ＜ α ＜ π ＜ 2π−α ＜ 2π

    ２つの解α，2π−α の場合，どちらが b(τ) であるのかの判別が問題になる。
    実際，α が０, π に近いときは，見た目では判別できない。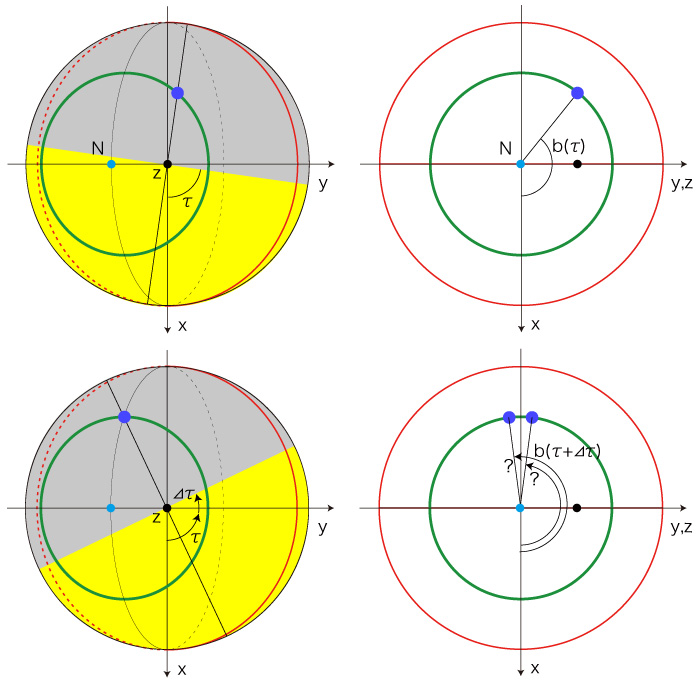
北中の場合


日出の場合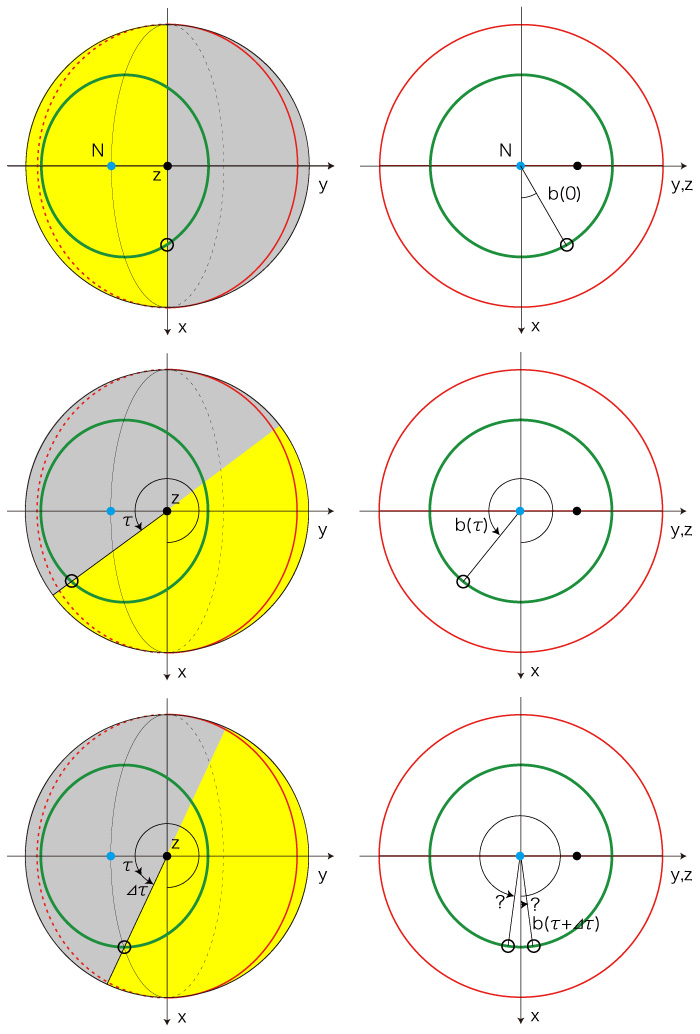

    ２つの解のどちらが適する解であるかの判別は，以下がこれの方法になる。

    はじめに， \[ cos( b(\tau_0) ) = 1 \\ cos( b(\tau_{\pi}) ) = -1 \] となる \( \tau_0), \ \tau_{\pi} \) を求める。

    そして，つぎのように判定する：
    (1) 0 < b(0) < π のとき
      (1.1) b(0) < α のとき
        (1.1.1) τ< \( \tau_{\pi} \) ならば，b(τ) ＝ α
        (1.1.2) τ> \( \tau_{\pi} \) ならば，b(τ) ＝ 2π−α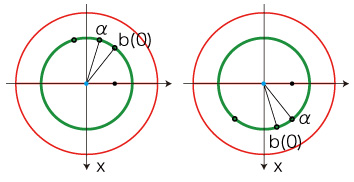
      (1.2) α< b(0) のとき
        (1.2.1) τ< \(\tau_0 \) ならば，b(τ) ＝ 2π−α
        (1.2.2) τ> \(\tau_0 \) ならば，b(τ) ＝ α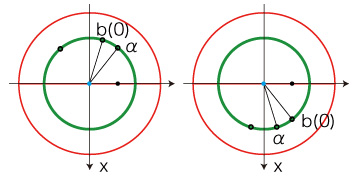

    (2) π < b(0) < 2π のとき
      (2.1) b(0) < 2π−α のとき
        (2.1.1) τ< \(\tau_0 \) ならば，b(τ) ＝ 2π−α
        (2.1.2) τ> \(\tau_0 \) ならば，b(τ) ＝ α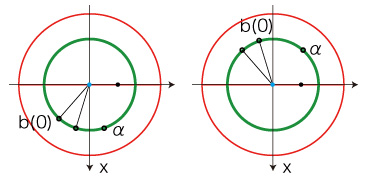
      (2.2) 2π−α < b(0) のとき
        (2.2.1) τ< \(\tau_{\pi} \) ならば，b(τ) ＝ α
        (2.2.2) τ> \(\tau_{\pi} \) ならば，b(τ) ＝ 2π−α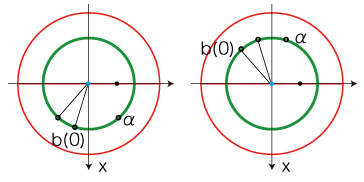



"; ?>