公転角がτのときの,緯度aの南中の経度は? 「南中の直交座標計算式」で,つぎを得ている: x=acτs√1−(ns)2(τc)2 そして,「自転軸系経度緯度と公転軸系直交座標の変換式」で,つぎを得ている: x=acbc よって, bc=τs√1−(ns)2(τc)2 (bs)2=1−(bc)2=1−(τs)21−(ns)2(τc)2=1−(ns)2(τc)2−(τs)21−(ns)2(τc)2=(τc)2−(ns)2(τc)21−(ns)2(τc)2=(nc)2(τc)21−(ns)2(τc)2 bs>0 は 0<b<π のときで,そしてこのときは 1/2π<τ<3/2π であり,τc<0。 よって,つぎのようになる: bs=−ncτc√1−(ns)2(τc)2 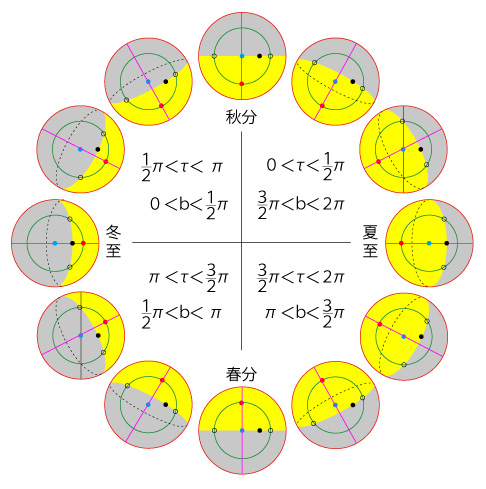
公転角がτのときの,緯度aの南中の経度bは, bc=τs√1−(ns)2(τc)2 bs=−ncτc√1−(ns)2(τc)2 |