公転角がτのときの,緯度aの日の出・日の入りの地点の座標は? はじめに,つぎを条件として措くことが必要になる (以下の推論の中でこのことがわかってくる): \[ a > n \\ a + n < \frac{\pi}{2} \\ \] 簡単のため \[ n_s = sin(n), \ \ n_c = cos(n) \\ a_s = sin(a), \ \ a_c = cos(a) \\ \tau_s = sin(\tau), \ \ \tau_c = cos(\tau) \] とおく。 さらにこの簡略記法 \[ x_s = sin(x) \\ x_c = cos(x) \] を,一般のxに対しても用いるとする。 (1) τ= 1/2π, 3/2π のとき 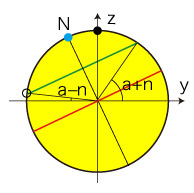
(1.2) τ= 3/2π (秋分) のとき 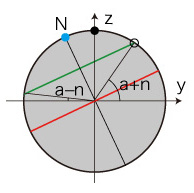
{2) τ≠ 0, π のとき 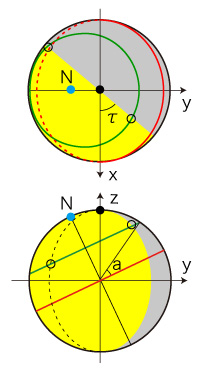
日出点Pの位置ベクトルを x とする。 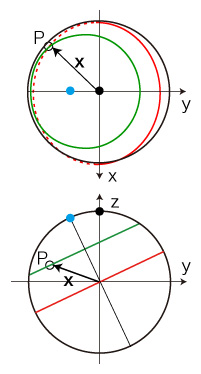
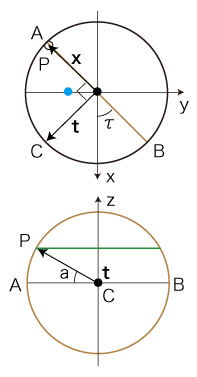
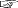 自転軸系経度緯度と公転軸系直交座標の変換式):
\[
a_s = -n_s \ y + n_c \ z \\
\]
よって,
\[
\begin{align}
z &= \frac{n_s \ y + a_s}{n_c} \\
&= \frac{n_s \tau_s \ x + a_s \tau_c}{n_c \tau_c}
\end{align}
\\ \ \\
\]
さらに
\[
\begin{align}
& x^2 + y^2 + z^2 = 1 \\
\Longrightarrow
& x^2
+ (\frac{\tau_s}{\tau_c} x)^2
+ (\frac{ n_s \tau_s \ x + a_s \tau_c }{ n_c \tau_c} )^2 = 1 \\
\Longrightarrow
& x^2
+ \frac{(\tau_s)^2}{(\tau_c)^2} \ x^2 \\
& \qquad
+ \frac{
(n_s \ \tau_s)^2 \ x^2
+ 2 n_s \ \tau_s \ \tau_c \ a_s \ x
+ (a_s)^2 (\tau_c)^2 }
{ (n_c)^2 (\tau_c)^2 }
= 1 \\
\ \\
\Longrightarrow
& ( ( n_c \tau_c )^2 + ( n_c \tau_s)^2 + (n_s \ \tau_s)^2 ) \ x^2 \\
& \qquad + 2 ( n_s \ a_s \ \tau_s \ \tau_c ) \ x \\
& \qquad + (a_s \tau_c)^2 = ( n_c \tau_c)^2 \\
\ \\
\Longrightarrow
& ( ( n_c \tau_c )^2 + (\tau_s)^2 ) \ x^2 \\
& \qquad + 2 ( n_s \ a_s \ \tau_s \ \tau_c ) \ x \\
& \qquad + (a_s \tau_c)^2 - ( n_c \tau_c)^2 = 0\\
\ \\
\Longrightarrow
& ( ( n_c \tau_c )^2 + 1 - (\tau_c)^2 ) \ x^2 \\
& \qquad + 2 ( n_s \ a_s \ \tau_s \ \tau_c ) \ x \\
& \qquad + ( (a_s )^2 - ( n_c)^2 ) (\tau_c)^2 = 0\\
\ \\
\Longrightarrow
& ( 1 - (n_s)^2 (\tau_c)^2 ) \ x^2 \\
& \qquad + 2 ( n_s \ a_s \ \tau_s \ \tau_c ) \ x \\
& \qquad + ( (a_s )^2 - ( n_c)^2 ) (\tau_c)^2 = 0\\
\ \\
\Longrightarrow
&x = \frac{ - n_s \ a_s \ \tau_s \ \tau_c \pm \sqrt{D}}{1 - (n_s)^2 (\tau_c)^2} \\
\ \\
&D = ( n_s a_s \tau_s \tau_c )^2 -
(1 - (n_s)^2 (\tau_c)^2)
( (a_s )^2 - ( n_c)^2 ) (\tau_c)^2 \\
\ \\
&\quad = ( n_s)^2 (a_s)^2 (\tau_s )^2 (\tau_c)^2 - \\
&\quad \quad
( (1 - (n_s)^2 (\tau_c)^2 ) (a_s)^2
- ( 1 - (n_s)^2 (\tau_c)^2 ) (n_c)^2) (\tau_c)^2 \\
\ \\
&\quad = ( n_s)^2 (a_s )^2 (\tau_s )^2 (\tau_c)^2 - \\
&\quad \quad
( (a_s)^2 - (n_s)^2 (a_s)^2 (\tau_c)^2
- ( n_c )^2 + (n_s)^2 (\tau_c)^2 (n_c)^2 ) (\tau_c)^2\\
\ \\
&\quad = ( ( n_s)^2 (a_s )^2 (\tau_s)^2
- (a_s)^2 + (n_s)^2 (a_s)^2 (\tau_c)^2
+ ( n_c )^2 - (n_s)^2 (\tau_c)^2 (n_c)^2 )
(\tau_c)^2\\
\ \\
&\quad = ( ( n_c )^2 + ( n_s)^2 (a_s )^2 (\tau_s )^2 + (n_s)^2 (a_s)^2 (\tau_c)^2
- (a_s)^2 - (n_s)^2 (\tau_c)^2 (n_c)^2 )
(\tau_c)^2\\
\ \\
&\quad = ( ( n_c )^2+ ( n_s)^2 (a_s )^2 - (a_s)^2 - (n_s)^2 (\tau_c)^2 (n_c)^2 )
(\tau_c)^2\\
\ \\
&\quad = ( ( n_c )^2 - ( 1 - (n_s)^2) (a_s )^2 - (n_s)^2 (\tau_c)^2 (n_c)^2 )
(\tau_c)^2\\
\ \\
&\quad = ( ( n_c )^2 - (n_c)^2 (a_s)^2 - (n_s)^2 (\tau_c)^2 (n_c)^2 )
(\tau_c)^2\\
\ \\
&\quad = ( (1 - (a_s)^2) - (n_s)^2 (\tau_c)^2 )
(n_c)^2 (\tau_c)^2\\
\ \\
&\quad = ( (a_c)^2 - (n_s)^2 (\tau_c)^2 )
(n_c)^2 (\tau_c)^2\\
\end{align}
\\
\]
はじめに a + n < π/2 を条件として措いたが,このとき
\[
\begin{align}
& a < \frac{\pi}{2} - n \\
\Longrightarrow \ \
& a_c > cos(\frac{\pi}{2} - n) = n_s \\
\Longrightarrow \ \
& D > 0 \\
\end{align}
\] 自転軸系経度緯度と公転軸系直交座標の変換式):
\[
a_s = -n_s \ y + n_c \ z \\
\]
よって,
\[
\begin{align}
z &= \frac{n_s \ y + a_s}{n_c} \\
&= \frac{n_s \tau_s \ x + a_s \tau_c}{n_c \tau_c}
\end{align}
\\ \ \\
\]
さらに
\[
\begin{align}
& x^2 + y^2 + z^2 = 1 \\
\Longrightarrow
& x^2
+ (\frac{\tau_s}{\tau_c} x)^2
+ (\frac{ n_s \tau_s \ x + a_s \tau_c }{ n_c \tau_c} )^2 = 1 \\
\Longrightarrow
& x^2
+ \frac{(\tau_s)^2}{(\tau_c)^2} \ x^2 \\
& \qquad
+ \frac{
(n_s \ \tau_s)^2 \ x^2
+ 2 n_s \ \tau_s \ \tau_c \ a_s \ x
+ (a_s)^2 (\tau_c)^2 }
{ (n_c)^2 (\tau_c)^2 }
= 1 \\
\ \\
\Longrightarrow
& ( ( n_c \tau_c )^2 + ( n_c \tau_s)^2 + (n_s \ \tau_s)^2 ) \ x^2 \\
& \qquad + 2 ( n_s \ a_s \ \tau_s \ \tau_c ) \ x \\
& \qquad + (a_s \tau_c)^2 = ( n_c \tau_c)^2 \\
\ \\
\Longrightarrow
& ( ( n_c \tau_c )^2 + (\tau_s)^2 ) \ x^2 \\
& \qquad + 2 ( n_s \ a_s \ \tau_s \ \tau_c ) \ x \\
& \qquad + (a_s \tau_c)^2 - ( n_c \tau_c)^2 = 0\\
\ \\
\Longrightarrow
& ( ( n_c \tau_c )^2 + 1 - (\tau_c)^2 ) \ x^2 \\
& \qquad + 2 ( n_s \ a_s \ \tau_s \ \tau_c ) \ x \\
& \qquad + ( (a_s )^2 - ( n_c)^2 ) (\tau_c)^2 = 0\\
\ \\
\Longrightarrow
& ( 1 - (n_s)^2 (\tau_c)^2 ) \ x^2 \\
& \qquad + 2 ( n_s \ a_s \ \tau_s \ \tau_c ) \ x \\
& \qquad + ( (a_s )^2 - ( n_c)^2 ) (\tau_c)^2 = 0\\
\ \\
\Longrightarrow
&x = \frac{ - n_s \ a_s \ \tau_s \ \tau_c \pm \sqrt{D}}{1 - (n_s)^2 (\tau_c)^2} \\
\ \\
&D = ( n_s a_s \tau_s \tau_c )^2 -
(1 - (n_s)^2 (\tau_c)^2)
( (a_s )^2 - ( n_c)^2 ) (\tau_c)^2 \\
\ \\
&\quad = ( n_s)^2 (a_s)^2 (\tau_s )^2 (\tau_c)^2 - \\
&\quad \quad
( (1 - (n_s)^2 (\tau_c)^2 ) (a_s)^2
- ( 1 - (n_s)^2 (\tau_c)^2 ) (n_c)^2) (\tau_c)^2 \\
\ \\
&\quad = ( n_s)^2 (a_s )^2 (\tau_s )^2 (\tau_c)^2 - \\
&\quad \quad
( (a_s)^2 - (n_s)^2 (a_s)^2 (\tau_c)^2
- ( n_c )^2 + (n_s)^2 (\tau_c)^2 (n_c)^2 ) (\tau_c)^2\\
\ \\
&\quad = ( ( n_s)^2 (a_s )^2 (\tau_s)^2
- (a_s)^2 + (n_s)^2 (a_s)^2 (\tau_c)^2
+ ( n_c )^2 - (n_s)^2 (\tau_c)^2 (n_c)^2 )
(\tau_c)^2\\
\ \\
&\quad = ( ( n_c )^2 + ( n_s)^2 (a_s )^2 (\tau_s )^2 + (n_s)^2 (a_s)^2 (\tau_c)^2
- (a_s)^2 - (n_s)^2 (\tau_c)^2 (n_c)^2 )
(\tau_c)^2\\
\ \\
&\quad = ( ( n_c )^2+ ( n_s)^2 (a_s )^2 - (a_s)^2 - (n_s)^2 (\tau_c)^2 (n_c)^2 )
(\tau_c)^2\\
\ \\
&\quad = ( ( n_c )^2 - ( 1 - (n_s)^2) (a_s )^2 - (n_s)^2 (\tau_c)^2 (n_c)^2 )
(\tau_c)^2\\
\ \\
&\quad = ( ( n_c )^2 - (n_c)^2 (a_s)^2 - (n_s)^2 (\tau_c)^2 (n_c)^2 )
(\tau_c)^2\\
\ \\
&\quad = ( (1 - (a_s)^2) - (n_s)^2 (\tau_c)^2 )
(n_c)^2 (\tau_c)^2\\
\ \\
&\quad = ( (a_c)^2 - (n_s)^2 (\tau_c)^2 )
(n_c)^2 (\tau_c)^2\\
\end{align}
\\
\]
はじめに a + n < π/2 を条件として措いたが,このとき
\[
\begin{align}
& a < \frac{\pi}{2} - n \\
\Longrightarrow \ \
& a_c > cos(\frac{\pi}{2} - n) = n_s \\
\Longrightarrow \ \
& D > 0 \\
\end{align}
\]
xが \[ x = \frac{ - n_s \ a_s \ \tau_s \ \tau_c \pm n_c \tau_c \sqrt{(a_c)^2 - (n_s)^2 (\tau_c)^2}}{1 - (n_s)^2 (\tau_c)^2} \] と確定したところで, \[ \begin{align} y & = \frac{\tau_s}{\tau_c} x = \frac{ - n_s \ a_s \ (\tau_s)^2 \pm n_c \tau_s \sqrt{(a_c)^2 - (n_s)^2 (\tau_c)^2}}{1 - (n_s)^2 (\tau_c)^2} \\ \ \\ z & = \frac{n_s \ y + a_s}{n_c} \\ \ \\ & = \frac{ - (n_s)^2 \ a_s \ (\tau_s)^2 \pm n_s n_c \tau_s \sqrt{(a_c)^2 - (n_s)^2 (\tau_s)^2} + a_s (1 - (n_s)^2 (\tau_c)^2) } {n_c \ (1 - (n_s)^2 (\tau_c)^2)} \\ \ \\ & = \frac{ - (n_s)^2 \ a_s \ (\tau_s)^2 \pm n_s n_c \tau_s \sqrt{(a_c)^2 - (n_s)^2 (\tau_s)^2} + a_s ( 1 - (n_s)^2 (1 - (\tau_s)^2 ) } {n_c \ (1 - (n_s)^2 (\tau_c)^2)} \\ \ \\ & = \frac{ - (n_s)^2 \ a_s \ (\tau_s)^2 \pm n_s n_c \tau_s \sqrt{(a_c)^2 - (n_s)^2 (\tau_s)^2} + a_s ( 1 - (n_s)^2 + (n_s)^2 (\tau_s)^2 ) } {n_c \ (1 - (n_s)^2 (\tau_c)^2)} \\ \ \\ & = \frac{ - (n_s)^2 \ a_s \ (\tau_s)^2 \pm n_s n_c \tau_s \sqrt{(a_c)^2 - (n_s)^2 (\tau_s)^2} + a_s (n_c)^2 + a_s (n_s)^2 (\tau_s)^2 } {n_c \ (1 - (n_s)^2 (\tau_c)^2)} \\ \ \\ & = \frac{ n_c a_s \pm n_s \tau_s \sqrt{(a_c)^2 - (n_s)^2 (\tau_s)^2}} {1 - (n_s)^2 (\tau_c)^2} \end{align} \]
日入
|