運動は,時間 \( t \) の位置と速度で表現される。
位置を表す方法は,座標である。
速度は,時間に対する位置の変化率である。
学校で習う座標は,空間座標だと x-y-z。
理系だと,さらに r-θ-φ を習ったかも知れない。
x-y-z と r-θ-φ の関係
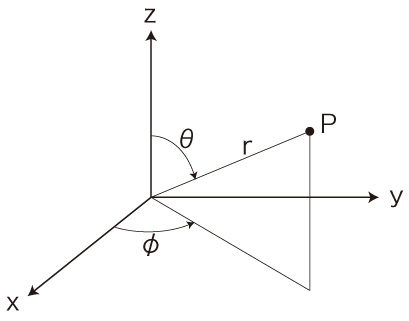
ここで,空間座標の一般表現として,
\[ ( q_1, q_2, \cdots, q_f )
\]
を用いることにする。
──空間もf次元に一般化した。
この座標に対する速度──時間に対する位置の変化率──は,
\[
( \frac{ d q_1 }{ dt }\,\ \frac{ d q_2}{ dt }\,\ \cdots,\ \frac{ d q_f }{ dt } )
\]
ここで
\[
\dot{q}_i = \frac{ d q_i }{ dt }
\]
と表すことにすると,速度がつぎの表現になる:
\[ ( \dot{q}_1, \dot{q}_2, \cdots, \dot{q}_f )
\]
例:ニュートン力学の運動方程式
これは,つぎのようになる:
\[
m \ddot{x} = F_x \quad \quad \ddot{x} = \frac{ d \dot{x} }{ dt }\ = \frac{ d^2 x }{ dt^2 } \\
m \ddot{y} = F_y \quad \quad \ddot{y} = \frac{ d \dot{y} }{ dt }\ = \frac{ d^2 y }{ dt^2 } \\
m \ddot{z} = F_z \quad \quad \ddot{z} = \frac{ d \dot{z} }{ dt }\ = \frac{ d^2 z }{ dt^2 }
\]
ここで,\( m \) は質量,\( F_x, F_y, F_z \) は力。
そしてこの運動方程式では,運動エネルギー \( T( \dot{x}, \dot{y}, \dot{z} ) \) と位置エネルギー \( V( x, y, z ) \) の概念がつぎのように立てられている:
\[
T = \frac{ 1 }{ 2 }\ m\ ( \dot{x}^2 + \dot{y}^2 + \dot{z}^2 ) \\
\ \\ \ \\
F_x = - \frac{ \partial V }{ \partial x } \\
F_y = - \frac{ \partial V }{ \partial y } \\
F_z = - \frac{ \partial V }{ \partial z }
\]
上の例では,運動を x-y-z 座標に対する運動方程式で表現した。
その運動方程式は,運動を別の座標──例えば,r-θ-φ ──で表現すると,まったく別の形に変わる。
そして,r-θ-φで運動方程式を表現するときは,x-y-z で表現した運動方程式に
\[
x = x( r, \theta, \phi ) \\
y = y( r, \theta, \phi ) \\
z = z( r, \theta, \phi )
\]
の代入計算をするわけであるが,これは計算量がひどくなる。
実際,計算がなんとか手に負えるのは,簡単な運動方程式に限る。
代入計算方式の座標変換は,一般に「使えない」となる。
この「運動方程式の形が変わる」「座標変換の計算が手に負えなくなる」を,「不都合」と考えよう。
そして,「座標を変えても形が変わらない運動方程式はないか?」と考えることにする。
このとき出てくるのが,ラグランジアンというわけである。
ラグランジアンとは,関数
\[
L( q_1, \cdots, q_f; \dot{q}_1, \cdots, \dot{q}_f )
\]
で,つぎの方程式が運動方程式になるようにつくられるものである:
\[
\frac{ d }{ dt }\ \bigl( \frac{ \partial L }{ \partial \dot{q}_i }\ \bigr) - \frac{ \partial L }{ \partial q_i }\ = 0 \quad \quad ( i = 1, 2, \cdots, f )
\]
ラグランジアン \( L( q_1, \cdots, q_f; \dot{q}_1, \cdots, \dot{q}_f ) \) に対する上の形の方程式を,「オイラー=ラグランジュの方程式」と呼ぶ。
例:ニュートン力学の運動方程式
\[
m \ddot{x} = - \frac{ \partial V }{ \partial x } \\
m \ddot{y} = - \frac{ \partial V }{ \partial y } \\
m \ddot{z} = - \frac{ \partial V }{ \partial z }
\]
に対し,つぎのように定めた \( L( x, y, z; \dot{x}, \dot{y}, \dot{z} ) \) はラグランジアンになる:
即ち,\( L \) のオイラー=ラグランジュの方程式
\[
\frac{ d }{ dt }\ \bigl( \frac{ \partial L }{ \partial \dot{x} }\ \bigr)
- \frac{ \partial L }{ \partial x } = 0 \\
\frac{ d }{ dt }\ \bigl( \frac{ \partial L }{ \partial \dot{y} }\ \bigr)
- \frac{ \partial L }{ \partial y } = 0 \\
\frac{ d }{ dt }\ \bigl( \frac{ \partial L }{ \partial \dot{z} }\ \bigr)
- \frac{ \partial L }{ \partial z } = 0
\]
が,運動方程式が同じになる。
実際,
\[
\frac{ d }{ dt }\ \bigl( \frac{ \partial L }{ \partial \dot{x} }\ \bigr)
- \frac{ \partial L }{ \partial x } \\
= \frac{ d }{ dt }\ \bigl( \frac{ \partial T }{ \partial \dot{x} }\ - \frac{ \partial V }{ \partial \dot{x} }\ \bigr)
- \bigl( \frac{ \partial T }{ \partial x } - \frac{ \partial V }{ \partial x }\ \bigr) \\
= \frac{ d }{ dt }\ ( m \dot{x} - 0 )
- \bigl( 0 + F_x ) \\
= m \ \ddot{x} - F_x
\]
よって,
\[
\frac{ d }{ dt }\ \bigl( \frac{ \partial L }{ \partial \dot{x} }\ \bigr)
- \frac{ \partial L }{ \partial x } = 0
\Longleftrightarrow
m \ddot{x} = F_x
\]
同様に
\[
\frac{ d }{ dt }\ \bigl( \frac{ \partial L }{ \partial \dot{y} }\ \bigr)
- \frac{ \partial L }{ \partial y } = 0
\Longleftrightarrow
m \ddot{y} = F_y \\
\frac{ d }{ dt }\ \bigl( \frac{ \partial L }{ \partial \dot{z} }\ \bigr)
- \frac{ \partial L }{ \partial z } = 0
\Longleftrightarrow
m \ddot{z} = F_z \\
\]
ラグランジアンは,オイラー=ラグランジュ方程式が「座標を変えても形が変わらない運動方程式」になるように,つくられるものである。
ここで「座標を変えても形が変わらない運動方程式」の意味は:
運動方程式を,特定の座標 \( ( q_1, \cdots, q_f ) \) で表現する。
この方程式を導くラグランジアン \( L( q_1, \cdots, q_f; \dot{q}_1, \cdots, \dot{q}_f ) \) をつくることができたとする。
このとき,別の座標 \( ( Q_1, \cdots, Q_f ) \) による運動方程式の表現が,つぎのようにして得られる:
\( L( q_1, \cdots, q_f; \dot{q}_1, \cdots, \dot{q}_f ) \) の \( q_1, \cdots, q_f, \dot{q}_1, \cdots, \dot{q}_f \) に,\( Q_1, \cdots, Q_f, \dot{Q}_1, \cdots, \dot{Q}_f \) を代入。
するとその式 \( K( Q_1, \cdots, Q_f; \dot{Q}_1, \cdots, \dot{Q}_f ) \) がラグランジアンになっている。
即ち,これのオイラー=ラグランジュ方程式が,座標 \( ( Q_1, \cdots, Q_f ) \) で表した運動方程式になっている。
そんなうまい話があるのかと思うだろうが,現にいろいろな力学分野でラグランジアンが開発されている。
尤も,うまい話である分,ラグランジアンをつくるのは実際のところたいへんということである。
|
