このとき,別の座標がこのラグランジアンの正準座標かどうかを判定する直接の方法は,
オイラー=ラグランジュ方程式への代入計算の結果 このときの計算は,たいへんである。 そして,「座標に依存しない」を売りにしているのがラグランジアンなのに,この計算は「座標に依存するかどうか」を調べているわけであり,なんとも気が利かない。 そこで,「直接計算ではない判定法はないか?」となる。 ここに,ポワソン括弧を使った判定法の登場となる。 但し,これは「簡単な判定法」というわけにはいかない。 計算量は,たいへんなままである。 実際,ポワソン括弧を使った判定法の売りは,「直接計算が無理な場合にも使える」である。 そしてその判定法だが,つぎの通り:
ここでポアソン括弧の定義は,
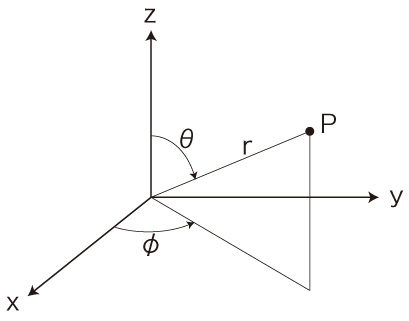
\[ x = r\ sin \theta\ cos \phi \\ y = r\ sin \theta\ sin \phi \\ z = r\ cos \theta \\ \] \[ \dot{x} = \frac{ \partial x }{ \partial r }\ \dot{r} + \frac{ \partial x }{ \partial \theta }\ \dot{\theta} + \frac{ \partial x }{ \partial \phi }\ \dot{\phi} \\ = sin \theta\ cos \phi\ \dot{r} + r\ cos \theta\ cos \phi\ \dot{\theta} - r\ sin \theta\ sin \phi\ \dot{\phi} \\ \ \\ \dot{y} = \frac{ \partial y }{ \partial r }\ \dot{r} + \frac{ \partial y }{ \partial \theta }\ \dot{\theta} + \frac{ \partial y }{ \partial \phi }\ \dot{\phi} \\ = sin \theta\ sin \phi\ \dot{r} + r\ cos \theta\ sin \phi\ \dot{\theta} + r\ sin \theta\ cos \phi\ \dot{\phi} \\ \ \\ \dot{z} = \frac{ \partial z }{ \partial r }\ \dot{r} + \frac{ \partial z }{ \partial \theta }\ \dot{\theta} \\ = cos \theta\ \dot{r} - r\ sin \theta\ \dot{\theta} \\ \] \[ L( x, y, z; \dot{x}, \dot{y}, \dot{z} ) \\ = \frac{ 1 }{ 2 }\ m\ ( \dot{x}^2 + \dot{y}^2 + \dot{z}^2 ) - V( x, y, z ) \\ \ \\ = \frac{ 1 }{ 2 }\ m\ ( \\ \quad\ ( \dot{r}\ sin \theta\ cos \phi + r\ \dot{\theta}\ cos \theta\ cos \phi - r\ \dot{\phi}\ \ sin \theta\ sin \phi )^2 \\ \quad\ + ( \dot{r}\ sin \theta\ sin \phi + r\ \dot{\theta}\ cos \theta\ sin \phi + r\ \dot{\phi}\ sin \theta\ cos \phi )^2 \\ \quad\ + ( \dot{r}\ cos \theta - r \dot{\theta}\ \ sin \theta )^2 \\ \quad\ ) \\ \quad\ - V( x, y, z ) \\ \ \\ = \frac{ 1 }{ 2 }\ m\ ( \\ \quad\ \dot{r}^2\ sin^2 \theta\ cos^2 \phi + r^2\ \dot{\theta}^2\ cos^2 \theta\ cos^2 \phi + r^2\ \dot{\phi}^2\ \ sin^2 \theta\ sin^2 \phi \\ \quad + 2\ r\ \dot{r}\ dot{\theta}\ cos \theta\ sin \theta\ cos^2 \phi - 2\ r^2\ \dot{\theta}\ \dot{\phi}\ cos \theta\ sin \theta\ cos \phi \ sin \phi - 2\ r\ \dot{\phi}\ \dot{r}\ \ sin^2 \theta\ cos \phi\ sin \phi \\ \quad + \dot{r}^2\ sin^2 \theta\ sin^2 \phi + r^2\ \dot{\theta}^2\ cos^2 \theta\ sin^2 \phi + r^2\ \dot{\phi}^2\ sin^2 \theta\ cos^2 \phi \\ \quad + 2\ r\ \dot{r}\ \dot{\theta}\ cos \theta\ sin \theta\ sin^2\phi + 2\ r^2\ \dot{\theta}\ \dot{\phi}\ cos \theta\ sin \theta\ cos \phi\ sin \phi + 2\ r\ \dot{\phi}\ \dot{r}\ sin^2 \theta\ cos \phi\ sin \phi \\ \quad + ( \dot{r}^2\ cos^2 \theta + r^2 \dot{\theta}^2\ \ sin^2 \theta \\ \quad - 2\ r\dot{r}\ \dot{\theta}\ cos \theta\ sin \theta \\ \quad\ ) \\ \quad\ - V( x, y, z ) \\ \ \\ = \frac{ 1 }{ 2 }\ m\ ( \\ \quad\ \dot{r}^2\ sin^2 \theta\ cos^2 \phi + \dot{r}^2\ sin^2 \theta\ sin^2 \phi + \dot{r}^2\ cos^2 \theta \\ \quad\ + r^2\ \dot{\theta}^2\ cos^2 \theta\ cos^2 \phi + r^2\ \dot{\theta}^2\ cos^2 \theta\ sin^2 \phi + r^2 \dot{\theta}^2\ sin^2 \theta \\ \quad\ + r^2\ \dot{\phi}^2\ \ sin^2 \theta\ sin^2 \phi + r^2\ \dot{\phi}^2\ sin^2 \theta\ cos^2 \phi \\ \quad\ + 2\ r\ \dot{r}\ \dot{\theta}\ cos \theta\ sin \theta\ cos^2 \phi + 2\ r\ \dot{r}\ \dot{\theta}\ cos \theta\ sin \theta\ sin^2\phi - 2\ r\dot{r}\ \dot{\theta}\ cos \theta\ sin \theta \\ \quad\ - 2\ r^2\ \dot{\theta}\ \dot{\phi}\ cos \theta\ sin \theta\ cos \phi \ sin \phi + 2\ r^2\ \dot{\theta}\ \dot{\phi}\ cos \theta\ sin \theta\ cos \phi\ sin \phi \\ \quad\ - 2\ r\ \dot{\phi}\ \dot{r}\ sin^2 \theta\ cos \phi\ sin \phi + 2\ r\ \dot{\phi}\ \dot{r}\ sin^2 \theta\ cos \phi\ sin \phi \\ \quad\ ) \\ \quad\ - V( x, y, z ) \\ \ \\ = \frac{ 1 }{ 2 }\ m\ ( \dot{r}^2 + r^2\ \dot{\theta}^2 + r^2\ \dot{\phi}^2\ sin^2 \theta ) - V( r, \theta, \phi ) \\ \] \[ p_r = \frac{ \partial L }{ \partial \dot{r} } = m\ \dot{r} \\ p_\theta = \frac{ \partial L }{ \partial \dot{\theta} } = m\ r^2\ \dot{\theta} \\ p_\phi = \frac{ \partial L }{ \partial \dot{\phi} } = m\ r^2\ \dot{\phi}\ sin^2 \theta \\ \] \[ \dot{r} = \frac{ p_r }{ m } \\ \dot{\theta} = \frac{ p_\theta }{ m\ r^2 } \\ \dot{\phi} = \frac{ p_\phi }{ m\ r^2\ sin^2 \theta } \\ \] \[ \begin{align} p_x &= m\ \dot{x} \\ &= m\ ( sin \theta\ cos \phi\ \dot{r} + r\ cos \theta\ cos \phi\ \dot{\theta} - r\ sin \theta\ sin \phi\ \dot{\phi} ) \\ &= p_r\ sin \theta\ cos \phi + \frac{ p_\theta }{ r }\ cos \theta\ cos \phi - \frac{ p_\phi }{ r\ sin \theta }\ \ sin \phi \\ \ \\ p_y &= m\ \dot{y} \\ &= m\ ( sin \theta\ sin \phi\ \dot{r} + r\ cos \theta\ sin \phi\ \dot{\theta} + r\ sin \theta\ cos \phi\ \dot{\phi} ) \\ &= p_r\ sin \theta\ sin \phi + \frac{ p_\theta }{ r }\ cos \theta\ sin \phi + \frac{ p_\phi }{ r\ sin \theta }\ cos \phi \\ \ \\ p_z &= m\ \dot{z} \\ &= m\ ( cos \theta\ \dot{r} - r\ sin \theta\ \dot{\theta} ) \\ &= p_r\ cos \theta - \frac{ p_\theta }{ r }\ \ sin \theta \\ \end{align} \] そして \[ x = r\ sin \theta\ cos \phi \\ y = r\ sin \theta\ sin \phi \\ z = r\ cos \theta \] より \[ \frac{ \partial x }{ \partial r } = sin \theta\ cos \phi \\ \frac{ \partial x }{ \partial \theta } = r\ cos \theta\ cos \phi \\ \frac{ \partial x }{ \partial \phi } = - r\ sin \theta\ sin \phi \\ \ \\ \ \\ \frac{ \partial y }{ \partial r } = sin \theta\ sin \phi \\ \frac{ \partial y }{ \partial \theta } = r\ cos \theta\ sin \phi \\ \frac{ \partial y }{ \partial \phi } = r\ sin \theta\ cos \phi \\ \ \\ \ \\ \frac{ \partial z }{ \partial r } = cos \theta \\ \frac{ \partial z }{ \partial \theta } = - r\ sin \theta \\ \frac{ \partial z }{ \partial \phi } = 0 \\ \ \\ \ \\ \frac{ \partial x }{ \partial p_r } = \frac{ \partial x }{ \partial p_\theta } = \frac{ \partial x }{ \partial p_\phi } = 0 \\ \ \\ \frac{ \partial y }{ \partial p_r } = \frac{ \partial y }{ \partial p_\theta } = \frac{ \partial y }{ \partial p_\phi } = 0 \\ \ \\ \frac{ \partial z }{ \partial p_r } = \frac{ \partial z }{ \partial p_\theta } = \frac{ \partial z }{ \partial p_\phi } = 0 \\ \] そして \[ p_x = p_r\ sin \theta\ cos \phi + \frac{ p_\theta }{ r }\ cos \theta\ cos \phi - \frac{ p_\phi }{ r\ sin \theta }\ \ sin \phi \] より \[ \frac{ \partial p_x }{ \partial r } = - \frac{ p_\theta }{ r^2 }\ cos \theta\ cos \phi + \frac{ p_\phi }{ r^2\ sin \theta }\ \ sin \phi \\ \frac{ \partial p_x }{ \partial \theta } = p_r\ cos \theta\ cos \phi - \frac{ p_\theta }{ r }\ sin \theta\ cos \phi + \frac{ p_\phi\ cos \theta }{ r\ sin^2 \theta }\ \ sin \phi \\ \frac{ \partial p_x }{ \partial \phi } = - p_r\ sin \theta\ sin \phi - \frac{ p_\theta }{ r }\ cos \theta\ sin \phi - \frac{ p_\phi }{ r\ sin \theta }\ \ cos \phi \\ \ \\ \ \\ \frac{ \partial p_x }{ \partial p_r } = sin \theta\ cos \phi \\ \frac{ \partial p_x }{ \partial p_\theta } = \frac{ 1 }{ r }\ cos \theta\ cos \phi \\ \frac{ \partial p_x }{ \partial p_\phi } = - \frac{ 1 }{ r\ sin \theta }\ \ sin \phi \\ \] そして \[ p_y = p_r\ sin \theta\ sin \phi + \frac{ p_\theta }{ r }\ cos \theta\ sin \phi + \frac{ p_\phi }{ r\ sin \theta }\ cos \phi \] より \[ \frac{ \partial p_y }{ \partial r } = - \frac{ p_\theta }{ r^2 }\ cos \theta\ sin \phi - \frac{ p_\phi }{ r^2\ sin \theta }\ cos \phi \\ \frac{ \partial p_y }{ \partial \theta } = p_r\ cos \theta\ sin \phi - \frac{ p_\theta }{ r }\ sin \theta\ sin \phi - \frac{ p_\phi\ cos \theta }{ r\ sin^2 \theta }\ cos \phi \\ \frac{ \partial p_y }{ \partial \phi } = p_r\ sin \theta\ cos \phi + \frac{ p_\theta }{ r }\ cos \theta\ cos \phi - \frac{ p_\phi }{ r\ sin \theta }\ sin \phi \\ \ \\ \ \\ \frac{ \partial p_y }{ \partial p_r } = sin \theta\ sin \phi \\ \frac{ \partial p_y }{ \partial p_\theta } = \frac{ 1 }{ r }\ cos \theta\ sin \phi \\ \frac{ \partial p_y }{ \partial p_\phi } = \frac{ 1 }{ r\ sin \theta }\ cos \phi \\ \] そして \[ p_z = p_r\ cos \theta - \frac{ p_\theta }{ r }\ \ sin \theta \] より \[ \frac{ \partial p_z }{ \partial r } = \frac{ p_\theta }{ r^2 }\ \ sin \theta \\ \frac{ \partial p_z }{ \partial \theta } = - p_r\ sin \theta - \frac{ p_\theta }{ r }\ \ cos \theta \\ \frac{ \partial p_z }{ \partial \phi } = 0 \\ \ \\ \ \\ \frac{ \partial p_z }{ \partial p_r } = cos \theta \\ \frac{ \partial p_z }{ \partial p_\theta } = - \frac{ 1 }{ r }\ \ sin \theta \\ \frac{ \partial p_z }{ \partial p_\phi } = 0 \\ \] そこで,\( x, y, z, p_s, p_y, p_z \) の \( r, \theta, \phi, p_r, p_\theta, p_\phi \) に対するポアソン括弧の計算が,以下のようになる: \[ [ \ x, x\ ] = 0 \\ [ \ y, y\ ] = 0 \\ [ \ z, z\ ] = 0 \\ \ \\ \ \\ [ \ x, y\ ] = \bigl( \frac{ \partial x }{ \partial r }\ \frac{ \partial y }{ \partial p_r } - \frac{ \partial x }{ \partial p_r }\ \frac{ \partial y }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial x }{ \partial \theta }\ \frac{ \partial y }{ \partial p_\theta } - \frac{ \partial x }{ \partial p_\theta }\ \frac{ \partial y }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial x }{ \partial \phi }\ \frac{ \partial y }{ \partial p_\phi } - \frac{ \partial x }{ \partial p_\phi }\ \frac{ \partial y }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( sin \theta\ cos \phi )\ 0 - 0\ ( sin \theta\ sin \phi ) \bigr) \\ + \bigl( ( r\ cos \theta\ cos \phi )\ 0 - 0\ ( r\ cos \theta\ sin \phi ) \bigr) \\ + \bigl( ( - r\ sin \theta\ sin \phi )\ 0 - 0\ ( r\ sin \theta\ cos \phi ) \bigr) \ \\ \ \\ = 0 \\ \ \\ \ \\ [ \ y, z\ ] = \bigl( \frac{ \partial y }{ \partial r }\ \frac{ \partial z }{ \partial p_r } - \frac{ \partial y }{ \partial p_r }\ \frac{ \partial z }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial y }{ \partial \theta }\ \frac{ \partial z }{ \partial p_\theta } - \frac{ \partial y }{ \partial p_\theta }\ \frac{ \partial z }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial y }{ \partial \phi }\ \frac{ \partial z }{ \partial p_\phi } - \frac{ \partial y }{ \partial p_\phi }\ \frac{ \partial z }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( sin \theta\ sin \phi )\ 0 - 0\ ( cos \theta ) \bigr) \\ + \bigl( ( r\ cos \theta\ sin \phi )\ 0 - 0\ ( - r\ sin \theta ) \bigr) \\ + \bigl( ( r\ sin \theta\ cos \phi )\ 0 - 0\ 0 \bigr) \ \\ \ \\ = 0 \\ \ \\ \ \\ [ \ z, x\ ] = \bigl( \frac{ \partial z }{ \partial r }\ \frac{ \partial x }{ \partial p_r } - \frac{ \partial z }{ \partial p_r }\ \frac{ \partial x }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial z }{ \partial \theta }\ \frac{ \partial x }{ \partial p_\theta } - \frac{ \partial z }{ \partial p_\theta }\ \frac{ \partial x }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial z }{ \partial \phi }\ \frac{ \partial x }{ \partial p_\phi } - \frac{ \partial z }{ \partial p_\phi }\ \frac{ \partial x }{ \partial \phi } \bigr) \\ = \bigl( ( cos \theta )\ 0 - 0\ ( sin \theta\ cos \phi ) \bigr) \\ + \bigl( ( - r\ sin \theta )\ 0 - 0\ ( r\ cos \theta\ cos \phi ) \bigr) \\ + \bigl( 0\ 0 - 0\ ( - r\ sin \theta\ sin \phi ) \bigr) \ \\ \ \\ = 0 \] \[ [ \ p_x, p_x\ ] = 0 \\ [ \ p_y, p_y\ ] = 0 \\ [ \ p_z, p_z\ ] = 0 \\ \ \\ \ \\ [ \ p_x, p_y\ ] = \bigl( \frac{ \partial p_x }{ \partial r }\ \frac{ \partial p_y }{ \partial p_r } - \frac{ \partial p_x }{ \partial p_r }\ \frac{ \partial p_y }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial p_x }{ \partial \theta }\ \frac{ \partial p_y }{ \partial p_\theta } - \frac{ \partial p_x }{ \partial p_\theta }\ \frac{ \partial p_y }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial p_x }{ \partial \phi }\ \frac{ \partial p_y }{ \partial p_\phi } - \frac{ \partial p_x }{ \partial p_\phi }\ \frac{ \partial p_y }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( - \frac{ p_\theta }{ r^2 }\ cos \theta\ cos \phi + \frac{ p_\phi }{ r^2\ sin \theta }\ \ sin \phi )\ ( sin \theta\ sin \phi ) \\ - ( sin \theta\ cos \phi )\ ( - \frac{ p_\theta }{ r^2 }\ cos \theta\ sin \phi - \frac{ p_\phi }{ r^2\ sin \theta }\ cos \phi ) \bigr) \\ \ \\ + \bigl( ( p_r\ cos \theta\ cos \phi - \frac{ p_\theta }{ r }\ sin \theta\ cos \phi + \frac{ p_\phi\ cos \theta }{ r\ sin^2 \theta }\ \ sin \phi )\ ( \frac{ 1 }{ r }\ cos \theta\ sin \phi ) \\ - ( \frac{ 1 }{ r }\ cos \theta\ cos \phi )\ ( p_r\ cos \theta\ sin \phi - \frac{ p_\theta }{ r }\ sin \theta\ sin \phi - \frac{ p_\phi\ cos \theta }{ r\ sin^2 \theta }\ cos \phi ) \bigr) \\ \ \\ + \bigl( ( - p_r\ sin \theta\ sin \phi - \frac{ p_\theta }{ r }\ cos \theta\ sin \phi - \frac{ p_\phi }{ r\ sin \theta }\ \ cos \phi )\ ( \frac{ 1 }{ r\ sin \theta }\ cos \phi ) \\ - ( - \frac{ 1 }{ r\ sin \theta }\ \ sin \phi )\ ( p_r\ sin \theta\ cos \phi + \frac{ p_\theta }{ r }\ cos \theta\ cos \phi - \frac{ p_\phi }{ r\ sin \theta }\ sin \phi ) \bigr) \ \\ \ \\ \ \\ = - \frac{ p_\theta }{ r^2 }\ cos \theta\ cos \phi\ ( sin \theta\ sin \phi ) + \frac{ p_\phi }{ r^2\ sin \theta }\ \ sin \phi\ ( sin \theta\ sin \phi ) ) \\ +( ( sin \theta\ cos \phi )\ \frac{ p_\theta }{ r^2 }\ cos \theta\ sin \phi + ( sin \theta\ cos \phi )\ \frac{ p_\phi }{ r^2\ sin \theta }\ cos \phi \\ + p_r\ cos \theta\ cos \phi\ ( \frac{ 1 }{ r }\ cos \theta\ sin \phi ) - \frac{ p_\theta }{ r }\ sin \theta\ cos \phi\ ( \frac{ 1 }{ r }\ cos \theta\ sin \phi ) + \frac{ p_\phi\ cos \theta }{ r\ sin^2 \theta }\ \ sin \phi\ ( \frac{ 1 }{ r }\ cos \theta\ sin \phi ) ) \\ - ( \frac{ 1 }{ r }\ cos \theta\ cos \phi )\ p_r\ cos \theta\ sin \phi + ( \frac{ 1 }{ r }\ cos \theta\ cos \phi )\ \frac{ p_\theta }{ r }\ sin \theta\ sin \phi + ( \frac{ 1 }{ r }\ cos \theta\ cos \phi )\ \frac{ p_\phi\ cos \theta }{ r\ sin^2 \theta }\ cos \phi \bigr) \\ - p_r\ sin \theta\ sin \phi\ ( \frac{ 1 }{ r\ sin \theta }\ cos \phi ) - \frac{ p_\theta }{ r }\ cos \theta\ sin \phi\ ( \frac{ 1 }{ r\ sin \theta }\ cos \phi ) - \frac{ p_\phi }{ r\ sin \theta }\ \ cos \phi\ ( \frac{ 1 }{ r\ sin \theta }\ cos \phi ) \\ + ( \frac{ 1 }{ r\ sin \theta }\ sin \phi )\ p_r\ sin \theta\ cos \phi + ( \frac{ 1 }{ r\ sin \theta }\ sin \phi )\ \frac{ p_\theta }{ r }\ cos \theta\ cos \phi - ( \frac{ 1 }{ r\ sin \theta }\ sin \phi )\ \frac{ p_\phi }{ r\ sin \theta }\ sin \phi \ \\ \ \\ \ \\ = - \frac{ p_\theta }{ r^2 }\ cos \theta\ sin \theta\ cos \phi\ sin \phi + \frac{ p_\phi }{ r^2 }\ \ sin^2 \phi \\ + \frac{ p_\theta }{ r^2 }\ cos \theta\ sin \theta\ cos \phi\ sin \phi + \frac{ p_\phi }{ r^2 }\ cos^2 \phi \\ + \frac{ p_r }{ r }\ cos^2 \theta\ sin \phi\ cos \phi - \frac{ p_\theta }{ r^2 }\ cos \theta\ sin \theta\ cos \phi\ sin \phi + \frac{ p_\phi }{ r^2\ sin^2 \theta } \ cos^2 \theta\ sin^2 \phi \\ - \frac{ p_r }{ r }\ cos^2 \theta\ cos \phi\ sin \phi + \frac{ p_\theta }{ r^2 }\ cos \theta\ sin \theta\ cos \phi\ sin \phi + \frac{ p_\phi }{ r^2\ sin^2 \theta}\ cos^2 \theta\ cos^2 \phi \\ - \frac{ p_r }{ r }\ cos \phi\ sin \phi - \frac{ p_\theta }{ r^2\ sin \theta }\ cos \theta\ cos \phi\ sin \phi - \frac{ p_\phi }{ r^2\ sin^2 \theta }\ cos^2 \phi \\ + \frac{ p_r }{ r }\ cos \phi \ sin \phi + \frac{ p_\theta }{ r^2\ sin \theta }\ cos \theta\ cos \phi \ sin \phi - \frac{ p_\phi }{ r^2\ sin^2 \theta }\ sin^2 \phi \\ \] \[ = \frac{ p_r }{ r }\ cos^2 \theta\ cos \phi\ sin \phi \\ - \frac{ p_r }{ r }\ cos^2 \theta\ cos \phi\ sin \phi \\ - \frac{ p_r }{ r }\ cos \phi\ sin \phi \\ + \frac{ p_r }{ r }\ cos \phi \ sin \phi \\ \ \\ \ \\ - \frac{ p_\theta }{ r^2 }\ cos \theta\ sin \theta\ cos \phi\ sin \phi \\ + \frac{ p_\theta }{ r^2 }\ cos \theta\ sin \theta\ cos \phi\ sin \phi \\ - \frac{ p_\theta }{ r^2 }\ cos \theta\ sin \theta\ cos \phi\ sin \phi \\ + \frac{ p_\theta }{ r^2 }\ cos \theta\ sin \theta\ cos \phi\ sin \phi \\ - \frac{ p_\theta }{ r^2\ sin \theta }\ cos \theta\ cos \phi\ sin \phi \\ + \frac{ p_\theta }{ r^2\ sin \theta }\ cos \theta\ cos \phi \ sin \phi \\ \ \\ \ \\ + \frac{ p_\phi }{ r^2 }\ \ sin^2 \phi \\ + \frac{ p_\phi }{ r^2 }\ cos^2 \phi \\ + \frac{ p_\phi }{ r^2\ sin^2 \theta } \ cos^2 \theta\ sin^2 \phi \\ + \frac{ p_\phi }{ r^2\ sin^2 \theta}\ cos^2 \theta\ cos^2 \phi \\ - \frac{ p_\phi }{ r^2\ sin^2 \theta }\ cos^2 \phi \\ - \frac{ p_\phi }{ r^2\ sin^2 \theta }\ sin^2 \phi \\ \ \\ \ \\ = \frac{ p_\phi }{ r^2 } \\ + \frac{ p_\phi }{ r^2\ sin^2 \theta } \ cos^2 \theta \\ - \frac{ p_\phi }{ r^2\ sin^2 \theta } \\ \ \\ \ \\ = \frac{ p_\phi }{ r^2\ sin^2 \theta }\ ( sin^2 \theta + \ cos^2 \theta - 1 ) \\ \ \\ \ \\ = 0 \] \[ [ \ p_y, p_z\ ] = \bigl( \frac{ \partial p_y }{ \partial r }\ \frac{ \partial p_z }{ \partial p_r } - \frac{ \partial p_y }{ \partial p_r }\ \frac{ \partial p_z }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial p_y }{ \partial \theta }\ \frac{ \partial p_z }{ \partial p_\theta } - \frac{ \partial p_y }{ \partial p_\theta }\ \frac{ \partial p_z }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial p_y }{ \partial \phi }\ \frac{ \partial p_z }{ \partial p_\phi } - \frac{ \partial p_y }{ \partial p_\phi }\ \frac{ \partial p_z }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( - \frac{ p_\theta }{ r^2 }\ cos \theta\ sin \phi - \frac{ p_\phi }{ r^2\ sin \theta }\ cos \phi )\ ( cos \theta ) \\ - ( sin \theta\ sin \phi )\ ( \frac{ p_\theta }{ r^2 }\ \ sin \theta ) \bigr) \\ + \bigl( ( p_r\ cos \theta\ sin \phi - \frac{ p_\theta }{ r }\ sin \theta\ sin \phi - \frac{ p_\phi\ cos \theta }{ r\ sin^2 \theta }\ cos \phi )\ ( - \frac{ 1 }{ r }\ \ sin \theta ) \\ - ( \frac{ 1 }{ r }\ cos \theta\ sin \phi )\ ( - p_r\ sin \theta - \frac{ p_\theta }{ r }\ \ cos \theta ) \bigr) \\ + \bigl( ( p_r\ sin \theta\ cos \phi + \frac{ p_\theta }{ r }\ cos \theta\ cos \phi - \frac{ p_\phi }{ r\ sin \theta }\ sin \phi )\ 0 \\ - ( \frac{ 1 }{ r\ sin \theta }\ cos \phi )\ 0 \bigr) \ \\ \ \\ \ \\ = \bigl( ( - \frac{ p_\theta }{ r^2 }\ cos^2 \theta\ sin \phi - \frac{ p_\phi }{ r^2\ sin \theta }\ cos \theta\ cos \phi ) \\ - ( \frac{ p_\theta }{ r^2 }\ \ sin^2 \theta\ sin \phi ) \bigr) \\ + \bigl( ( - \frac{ p_r }{ r }\ cos \theta\ sin \theta\ sin \phi + \frac{ p_\theta }{ r^2 }\ sin^2 \theta\ sin \phi + \frac{ p_\phi\ cos \theta }{ r^2\ sin \theta }\ cos \phi ) \\ +( \frac{ p_r }{ r }\ cos \theta\ sin \theta\ sin \phi )\ + \frac{ p_\theta }{ r^2 }\ \ cos^2 \theta\ sin \phi ) \bigr) \ \\ \ \\ = 0 \] \[ [ \ p_z, p_x\ ] = \bigl( \frac{ \partial p_z }{ \partial r }\ \frac{ \partial p_x }{ \partial p_r } - \frac{ \partial p_z }{ \partial p_r }\ \frac{ \partial p_x }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial p_z }{ \partial \theta }\ \frac{ \partial p_x }{ \partial p_\theta } - \frac{ \partial p_z }{ \partial p_\theta }\ \frac{ \partial p_x }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial p_z }{ \partial \phi }\ \frac{ \partial p_x }{ \partial p_\phi } - \frac{ \partial p_z }{ \partial p_\phi }\ \frac{ \partial p_x }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( \frac{ p_\theta }{ r^2 }\ \ sin \theta )\ ( sin \theta\ cos \phi ) - ( cos \theta )\ ( - \frac{ p_\theta }{ r^2 }\ cos \theta\ cos \phi + \frac{ p_\phi }{ r^2\ sin \theta }\ \ sin \phi ) \bigr) \\ + \bigl( ( - p_r\ sin \theta - \frac{ p_\theta }{ r }\ \ cos \theta )\ ( \frac{ 1 }{ r }\ cos \theta\ cos \phi ) \\ - ( - \frac{ 1 }{ r }\ \ sin \theta )\ ( p_r\ cos \theta\ cos \phi - \frac{ p_\theta }{ r }\ sin \theta\ cos \phi + \frac{ p_\phi\ cos \theta }{ r\ sin^2 \theta }\ \ sin \phi ) \bigr) \\ + \bigl( 0\ ( - \frac{ 1 }{ r\ sin \theta }\ \ sin \phi ) - 0\ ( - p_r\ sin \theta\ sin \phi - \frac{ p_\theta }{ r }\ cos \theta\ sin \phi - \frac{ p_\phi }{ r\ sin \theta }\ \ cos \phi ) \bigr) \ \\ \ \\ \ \\ = \bigl( ( \frac{ p_\theta }{ r^2 }\ \ sin^2 \theta\ cos \phi ) + ( \frac{ p_\theta }{ r^2 }\ cos^2 \theta\ cos \phi - \frac{ p_\phi }{ r^2\ sin \theta }\ cos \theta \ sin \phi ) \bigr) \\ + \bigl( ( - \frac{ p_r }{ r }\ cos \theta\ sin \theta\ cos \phi - \frac{ p_\theta }{ r^2 }\ cos^2 \theta\ cos \phi ) \\ + ( \frac{ p_r }{ r } \ cos \theta\ sin \theta\ cos \phi - \frac{ p_\theta }{ r^2 }\ sin^2 \theta\ cos \phi + \frac{ p_\phi\ cos \theta }{ r^2\ sin \theta }\ \ sin \phi ) \bigr) \ \\ \ \\ = 0 \] \[ [ \ x, p_x\ ] = \bigl( \frac{ \partial x }{ \partial r }\ \frac{ \partial p_x }{ \partial p_r } - \frac{ \partial x }{ \partial p_r }\ \frac{ \partial p_x }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial x }{ \partial \theta }\ \frac{ \partial p_x }{ \partial p_\theta } - \frac{ \partial x }{ \partial p_\theta }\ \frac{ \partial p_x }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial x }{ \partial \phi }\ \frac{ \partial p_x }{ \partial p_\phi } - \frac{ \partial x }{ \partial p_\phi }\ \frac{ \partial p_x }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( sin \theta\ cos \phi )\ \frac{ \partial p_x }{ \partial p_r } - 0\ \frac{ \partial p_x }{ \partial r } \bigr) \\ + \bigl( ( r\ cos \theta\ cos \phi )\ \frac{ \partial p_x }{ \partial p_\theta } - 0\ \frac{ \partial p_x }{ \partial \theta } \bigr) \\ + \bigl( ( - r\ sin \theta\ sin \phi )\ \frac{ \partial p_x }{ \partial p_\phi } - 0\ \frac{ \partial p_x }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( sin \theta\ cos \phi )\ ( sin \theta\ cos \phi ) \bigr) \\ + \bigl( ( r\ cos \theta\ cos \phi )\ ( \frac{ 1 }{ r }\ cos \theta\ cos \phi ) \bigr) \\ + \bigl( ( - r\ sin \theta\ sin \phi )\ ( - \frac{ 1 }{ r\ sin \theta }\ \ sin \phi ) \bigr) \ \\ \ \\ = 1 \] \[ [ \ x, p_y\ ] = \bigl( \frac{ \partial x }{ \partial r }\ \frac{ \partial p_y }{ \partial p_r } - \frac{ \partial x }{ \partial p_r }\ \frac{ \partial p_y }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial x }{ \partial \theta }\ \frac{ \partial p_y }{ \partial p_\theta } - \frac{ \partial x }{ \partial p_\theta }\ \frac{ \partial p_y }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial x }{ \partial \phi }\ \frac{ \partial p_y }{ \partial p_\phi } - \frac{ \partial x }{ \partial p_\phi }\ \frac{ \partial p_y }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( sin \theta\ cos \phi )\ \frac{ \partial p_y }{ \partial p_r } - 0\ \frac{ \partial p_y }{ \partial r } \bigr) \\ + \bigl( ( r\ cos \theta\ cos \phi )\ \frac{ \partial p_y }{ \partial p_\theta } - 0\ \frac{ \partial p_y }{ \partial \theta } \bigr) \\ + \bigl( ( - r\ sin \theta\ sin \phi )\ \frac{ \partial p_y }{ \partial p_\phi } - 0\ \frac{ \partial p_y }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( sin \theta\ cos \phi )\ ( sin \theta\ sin \phi ) \bigr) \\ + \bigl( ( r\ cos \theta\ cos \phi )\ ( \frac{ 1 }{ r }\ cos \theta\ sin \phi ) \bigr) \\ + \bigl( ( - r\ sin \theta\ sin \phi )\ ( \frac{ 1 }{ r\ sin \theta }\ cos \phi ) \bigr) \ \\ \ \\ = 0 \] \[ [ \ x, p_z\ ] = \bigl( \frac{ \partial x }{ \partial r }\ \frac{ \partial p_z }{ \partial p_r } - \frac{ \partial x }{ \partial p_r }\ \frac{ \partial p_z }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial x }{ \partial \theta }\ \frac{ \partial p_z }{ \partial p_\theta } - \frac{ \partial x }{ \partial p_\theta }\ \frac{ \partial p_z }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial x }{ \partial \phi }\ \frac{ \partial p_z }{ \partial p_\phi } - \frac{ \partial x }{ \partial p_\phi }\ \frac{ \partial p_z }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( sin \theta\ cos \phi )\ ( cos \theta ) - 0\ ( \frac{ p_\theta }{ r^2 }\ \ sin \theta ) \bigr) \\ + \bigl( ( r\ cos \theta\ cos \phi )\ ( - \frac{ 1 }{ r }\ \ sin \theta ) - 0\ ( - p_r\ sin \theta - \frac{ p_\theta }{ r }\ \ cos \theta ) \bigr) \\ + \bigl( ( - r\ sin \theta\ sin \phi )\ 0 - 0\ 0 \bigr) \ \\ \ \\ = \bigl( ( sin \theta\ cos \phi )\ ( cos \theta ) \bigr) \\ + \bigl( ( r\ cos \theta\ cos \phi )\ ( - \frac{ 1 }{ r }\ \ sin \theta ) \bigr) \\ + \bigl( ( - r\ sin \theta\ sin \phi )\ 0 \bigr) \ \\ \ \\ = 0 \] \[ [ \ y, p_x\ ] = \bigl( \frac{ \partial y }{ \partial r }\ \frac{ \partial p_x }{ \partial p_r } - \frac{ \partial y }{ \partial p_r }\ \frac{ \partial p_x }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial y }{ \partial \theta }\ \frac{ \partial p_x }{ \partial p_\theta } - \frac{ \partial y }{ \partial p_\theta }\ \frac{ \partial p_x }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial y }{ \partial \phi }\ \frac{ \partial p_x }{ \partial p_\phi } - \frac{ \partial y }{ \partial p_\phi }\ \frac{ \partial p_x }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( sin \theta\ sin \phi )\ \frac{ \partial p_x }{ \partial p_r } - 0\ \frac{ \partial p_x }{ \partial r } \bigr) \\ + \bigl( ( r\ cos \theta\ sin \phi )\ \frac{ \partial p_x }{ \partial p_\theta } - 0\ \frac{ \partial p_x }{ \partial \theta } \bigr) \\ + \bigl( ( r\ sin \theta\ cos \phi )\ \frac{ \partial p_x }{ \partial p_\phi } - 0\ \frac{ \partial p_x }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( sin \theta\ sin \phi )\ ( sin \theta\ cos \phi ) \bigr) \\ + \bigl( ( r\ cos \theta\ sin \phi )\ ( \frac{ 1 }{ r }\ cos \theta\ cos \phi ) \bigr) \\ + \bigl( ( r\ sin \theta\ cos \phi )\ ( - \frac{ 1 }{ r\ sin \theta }\ \ sin \phi ) \bigr) \ \\ \ \\ = 0 \] \[ [ \ y, p_y\ ] = \bigl( \frac{ \partial y }{ \partial r }\ \frac{ \partial p_y }{ \partial p_r } - \frac{ \partial y }{ \partial p_r }\ \frac{ \partial p_y }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial y }{ \partial \theta }\ \frac{ \partial p_y }{ \partial p_\theta } - \frac{ \partial y }{ \partial p_\theta }\ \frac{ \partial p_y }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial y }{ \partial \phi }\ \frac{ \partial p_y }{ \partial p_\phi } - \frac{ \partial y }{ \partial p_\phi }\ \frac{ \partial p_y }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( sin \theta\ sin \phi )\ \frac{ \partial p_y }{ \partial p_r } - 0\ \frac{ \partial p_y }{ \partial r } \bigr) \\ + \bigl( ( r\ cos \theta\ sin \phi )\ \frac{ \partial p_y }{ \partial p_\theta } - 0\ \frac{ \partial p_y }{ \partial \theta } \bigr) \\ + \bigl( ( r\ sin \theta\ cos \phi )\ \frac{ \partial p_y }{ \partial p_\phi } - 0\ \frac{ \partial p_y }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( sin \theta\ sin \phi )\ ( sin \theta\ sin \phi ) \bigr) \\ + \bigl( ( r\ cos \theta\ sin \phi )\ ( \frac{ 1 }{ r }\ cos \theta\ sin \phi ) \bigr) \\ + \bigl( ( r\ sin \theta\ cos \phi )\ ( \frac{ 1 }{ r\ sin \theta }\ cos \phi ) \bigr) \ \\ \ \\ = 1 \] \[ [ \ y, p_z\ ] = \bigl( \frac{ \partial y }{ \partial r }\ \frac{ \partial p_z }{ \partial p_r } - \frac{ \partial y }{ \partial p_r }\ \frac{ \partial p_z }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial y }{ \partial \theta }\ \frac{ \partial p_z }{ \partial p_\theta } - \frac{ \partial y }{ \partial p_\theta }\ \frac{ \partial p_z }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial y }{ \partial \phi }\ \frac{ \partial p_z }{ \partial p_\phi } - \frac{ \partial y }{ \partial p_\phi }\ \frac{ \partial p_z }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( sin \theta\ sin \phi )\ ( cos \theta ) - 0\ ( \frac{ p_\theta }{ r^2 }\ \ sin \theta ) \bigr) \\ + \bigl( ( r\ cos \theta\ sin \phi )\ ( - \frac{ 1 }{ r }\ \ sin \theta ) - 0\ ( - p_r\ sin \theta - \frac{ p_\theta }{ r }\ \ cos \theta ) \bigr) \\ + \bigl( ( r\ sin \theta\ cos \phi )\ 0 - 0\ 0 \bigr) \ \\ \ \\ = \bigl( ( sin \theta\ sin \phi )\ ( cos \theta ) \bigr) \\ + \bigl( ( r\ cos \theta\ sin \phi )\ ( - \frac{ 1 }{ r }\ \ sin \theta ) \bigr) \\ + \bigl( ( r\ sin \theta\ cos \phi )\ 0 \bigr) \ \\ \ \\ = 0 \] \[ [ \ z, p_x\ ] = \bigl( \frac{ \partial z }{ \partial r }\ \frac{ \partial p_x }{ \partial p_r } - \frac{ \partial z }{ \partial p_r }\ \frac{ \partial p_x }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial z }{ \partial \theta }\ \frac{ \partial p_x }{ \partial p_\theta } - \frac{ \partial z }{ \partial p_\theta }\ \frac{ \partial p_x }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial z }{ \partial \phi }\ \frac{ \partial p_x }{ \partial p_\phi } - \frac{ \partial z }{ \partial p_\phi }\ \frac{ \partial p_x }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( cos \theta )\ \frac{ \partial p_x }{ \partial p_r } - 0\ \frac{ \partial p_x }{ \partial r } \bigr) \\ + \bigl( ( - r\ sin \theta )\ \frac{ \partial p_x }{ \partial p_\theta } - 0\ \frac{ \partial p_x }{ \partial \theta } \bigr) \\ + \bigl( 0\ \frac{ \partial p_x }{ \partial p_\phi } - 0\ \frac{ \partial p_x }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( cos \theta )\ ( sin \theta\ cos \phi ) \bigr) \\ + \bigl( ( - r\ sin \theta )\ ( \frac{ 1 }{ r }\ cos \theta\ cos \phi ) \bigr) \ \ \ \\ \ \\ = 0 \] \[ [ \ z, p_y\ ] = \bigl( \frac{ \partial z }{ \partial r }\ \frac{ \partial p_y }{ \partial p_r } - \frac{ \partial z }{ \partial p_r }\ \frac{ \partial p_y }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial z }{ \partial \theta }\ \frac{ \partial p_y }{ \partial p_\theta } - \frac{ \partial z }{ \partial p_\theta }\ \frac{ \partial p_y }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial z }{ \partial \phi }\ \frac{ \partial p_y }{ \partial p_\phi } - \frac{ \partial z }{ \partial p_\phi }\ \frac{ \partial p_y }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( cos \theta )\ \frac{ \partial p_y }{ \partial p_r } - 0\ \frac{ \partial p_y }{ \partial r } \bigr) \\ + \bigl( ( - r\ sin \theta )\ \frac{ \partial p_y }{ \partial p_\theta } - 0\ \frac{ \partial p_y }{ \partial \theta } \bigr) \\ + \bigl( 0\ \frac{ \partial p_y }{ \partial p_\phi } - 0\ \frac{ \partial p_y }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( cos \theta )\ ( sin \theta\ sin \phi ) \bigr) \\ + \bigl( ( - r\ sin \theta )\ ( \frac{ 1 }{ r }\ cos \theta\ sin \phi ) \bigr) \ \ \ \\ \ \\ = 0 \] \[ [ \ z, p_z\ ] = \bigl( \frac{ \partial z }{ \partial r }\ \frac{ \partial p_z }{ \partial p_r } - \frac{ \partial z }{ \partial p_r }\ \frac{ \partial p_z }{ \partial r } \bigr) \ \ + \bigl( \frac{ \partial z }{ \partial \theta }\ \frac{ \partial p_z }{ \partial p_\theta } - \frac{ \partial z }{ \partial p_\theta }\ \frac{ \partial p_z }{ \partial \theta } \bigr) \ \ + \bigl( \frac{ \partial z }{ \partial \phi }\ \frac{ \partial p_z }{ \partial p_\phi } - \frac{ \partial z }{ \partial p_\phi }\ \frac{ \partial p_z }{ \partial \phi } \bigr) \ \\ \ \\ = \bigl( ( cos \theta )\ ( cos \theta ) - 0\ ( \frac{ p_\theta }{ r^2 }\ \ sin \theta ) \bigr) \\ + \bigl( ( - r\ sin \theta )\ ( - \frac{ 1 }{ r }\ \ sin \theta ) - 0\ ( - p_r\ sin \theta - \frac{ p_\theta }{ r }\ \ cos \theta ) \bigr) \\ + \bigl( 0\ 0 - 0\ 0 \bigr) \ \\ \ \\ = \bigl( ( cos \theta )\ ( cos \theta ) \bigr) \\ + \bigl( ( - r\ sin \theta )\ ( - \frac{ 1 }{ r }\ \ sin \theta ) \bigr) \ \ \ \\ \ \\ = 1 \] |