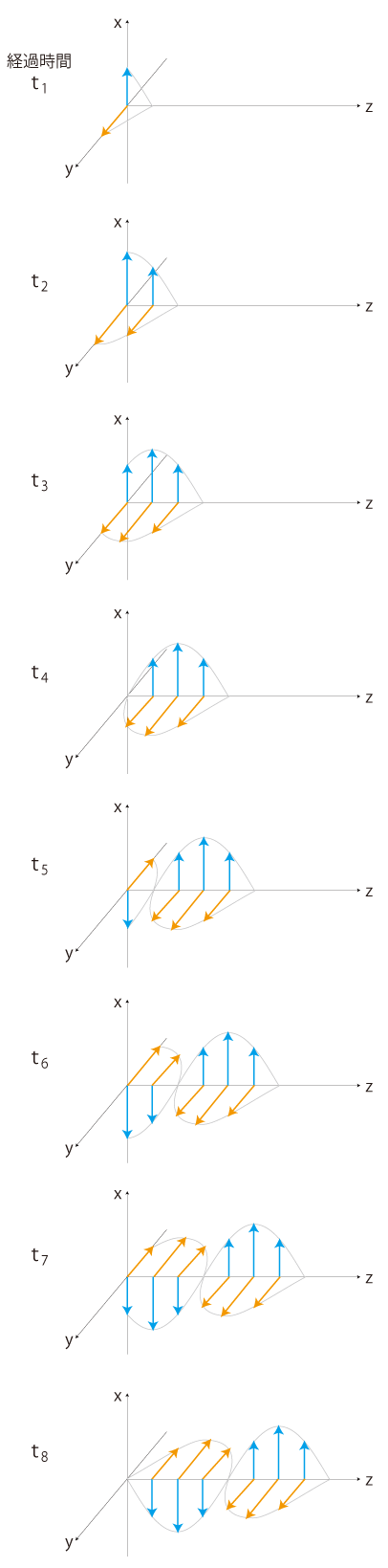
電場の伝播だけを抜き出すと: 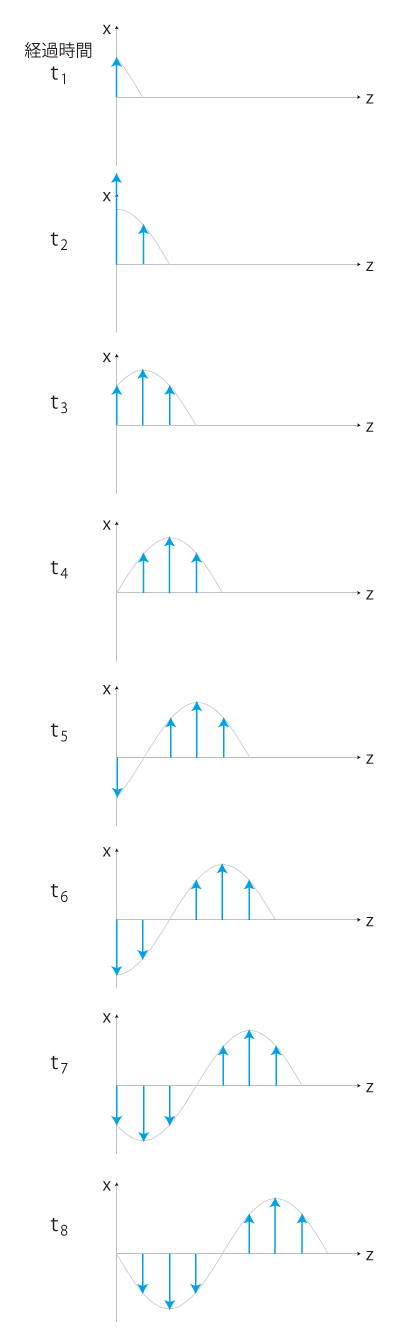
これを,つぎのグラフに表す: 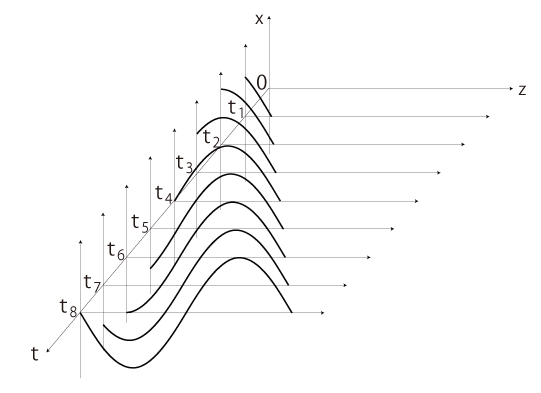
場所zの時間tの電場を \( \vec{E}(z,\,t) \) で表すと, \[ \vec{E}(z,\,t) = (E_x(z,\,t), \,0, \,0) \] であり,上のグラフは \( E_x(z,\,t) \) のグラフになっている。 場所z=0での電場の時間的変化は,\( E_x(0,\,t) \) のグラフになる: 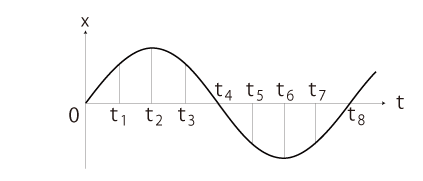
時間t=0では空間に波は現れていないが,以降の波の伝播を逆溯行するとき,つぎの波を潜在させていることになる──これを関数F(z) のグラフとする: 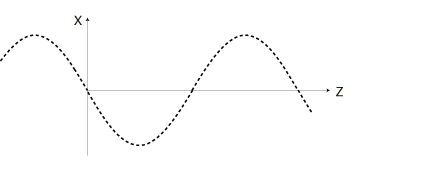
電場は,光速度cで伝わる。 よって,\( z=ct \) の関係にある \( (z,\,t) \) に対し,\( E_x(z,\,t) = E_x(0,\,0) = F(0) = 0 \) である。 したがって,\( E_x(z,\,t) \) のグラフが,つぎのようになる: 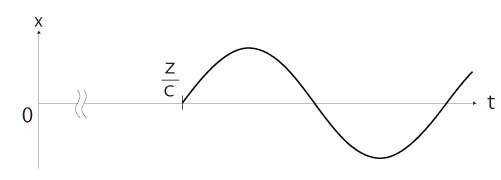
時間t固定 \[ E_x(z,\,t) = F( z - ct) \] 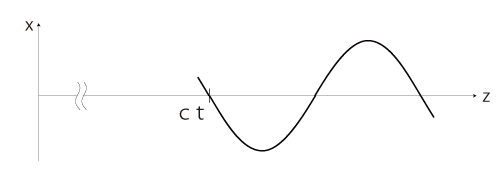
磁場も,これと同様に表現される。 |