Up 「力」の定義──ポテンシャルの gradient 作成: 2017-11-22
更新: 2017-11-26

    「場」の定義が成ると，空間にポテンシャルの等高線を書き入れることができる。
    空間に，傾斜がつくようになる。

    この「場」を，出発点にする。
    そして力ベクトルを，「斜面の下に落とす力」と見立てる。
    これは，力ベクトルを「斜面の下り勾配」として導入すればよい。

    二点間の移動の仕事量は，移動経路に沿って＜力ベクトルと微小移動ベクトルの内積＞を積分して求められた。
    そしてこの仕事量が，出発点のポテンシャルと到着点のポテンシャルの差になったわけである。
    いまこの積分は，力ベクトルが「斜面の下り勾配」の意味になったことで，「上下方向の移動距離を求める積分」になっている。
    即ち，つぎが実現されている：
      ＜高さ＞と＜勾配＞の関係を，力ベクトル場に同型に写す
      ──＜高さ＞がポテンシャルで，＜下り勾配＞が力


    点 \( \vec{x} \) での勾配は，つぎの定義になる：
      \[ grad \, \phi (\vec{x}) \,=\, \nabla \, \phi (\vec{x}) \,=\, ( \phi_x (\vec{x}),\, \phi_y (\vec{x}),\,\phi_z (\vec{x}) ) \]
    そこで，つぎが力の定義──点 \( \vec{x} \) における力ベクトル (物単位当たりに作用する力ベクトル) \( \vec{F} (\vec{x}) \) の定義──になる：
      \[ \vec{F} (\vec{x}) \,=\, - grad \, \phi (\vec{x}) \]


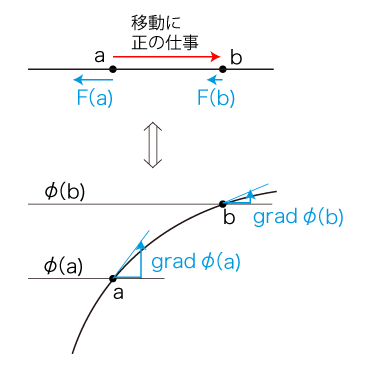
    各 \( \vec{x} \) には，「ポテンシャル」を意味するスカラー \( \phi(\vec{x}) \) と「力」を意味するベクトル \( \vec{F}(\vec{x}) \) が対応することになった。
    記号 \( \phi,\, \vec{F} \) を単独に取り出すときのこれの意味は，写像である：
      \( \phi \,:\, U \,\longrightarrow \ \ \mathbb{R^+} \)
      \( \vec{F} \,:\, U \,\longrightarrow \ \ V \) (力ベクトルの空間, ３次元)


    まとめ
    探求は，身近な「力」から抽象的な「ポテンシャル」の概念へと進む。
    そして「ポテンシャル」の導入で，つぎが要件になる：
      1. \( rot \,\vec{F}(\vec{x}) \,=\, 0 \)
      2. \( grad \,\phi(\vec{x}) \,=\, - \vec{F}(\vec{x}) \)

    (1) は，「二点間の移動の仕事は，経路に依らない」を述べている。
    これにより，「ポテンシャル」を，その下り勾配が「力」に相当するところのものとして導入できる。
    (2) は，「ポテンシャル」のこの導入を述べている。

    「場」の理論は，この順序を逆転する。
    「ポテンシャル」から「力」へ，になる。
    そして上の条件が，つぎの順番になる：
      1. \( rot \, grad \,\phi(\vec{x}) \,=\, 0 \)
      2. \( \vec{F}(\vec{x}) \,\equiv\, - grad \,\phi(\vec{x}) \)