物体の周りを流体が流れると,つぎのイメージの,速度や温度の境界層がつくられる:
HEXAGON『もっと流体基礎』から引用 (一部編集)
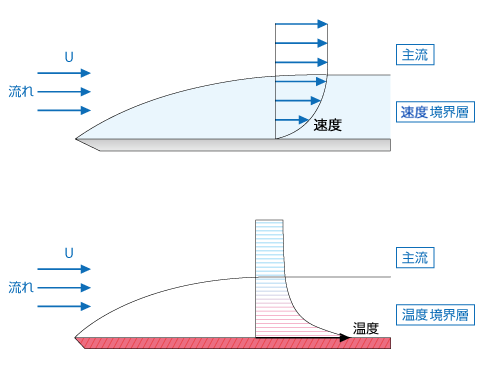
速度境界層は,「流体の粘性による力の遷移」で説明される。
そして,つぎの式 (「ニュートンの粘性法則」) に表現される:
\[
剪断応力\tau = -粘性係数\mu \times 速度勾配\frac{du}{dy} \\
\quad 次元(単位): Pa = Pa \cdot s \times \frac{m/s}{m}
\]
また温度境界層の方は,つぎの熱遷移の式 (「フーリエの法則) に表現される:
\[
熱流束 q = -熱伝導率\lambda \times 温度勾配\frac{dT}{dy} \\
\quad 次元(単位): \frac{W}{m^2} = \frac{W}{m \cdot K} \times \frac{K}{m}
\]
この2つの式に対しては,自ずと「相似」を見ることになる。
この相似は外観だけのもの?
否。2つの式は,つぎに示すように,量の次元 (単位) 込みで相似である:
先ず,N と W は,つぎのように相似である:,
\[
N = kg \cdot \frac{m}{s^2} = \bigl( kg \cdot \frac{m}{s} \bigr) / s \ :運動量遷移速度 \\
W =J / s \ :熱量遷移速度
\]
そして
\[
N \ (運動量遷移速度) \ \longleftrightarrow \ W \ (熱量遷移速度) \\
m / s \ (速度) \ \longleftrightarrow \ K \ (温度)
\]
の対応をつけるとき,
\[
Pa = \frac{N}{m^2}
\ \longleftrightarrow \
\frac{W}{m^2} \\
Pa \cdot s = \frac{N}{m^2} \cdot s = \frac{N}{m \cdot (m/s)}
\ \longleftrightarrow \
\frac{W}{m \cdot K} \\
\frac{m/s}{m}
\ \longleftrightarrow \
\frac{K}{m}
\]
以上のことを,ここではつぎのようにまとめておく:
- 運動と熱の間には,つぎの対応 (次元相似の対応) がある:
運動量 \( \longleftrightarrow \) 熱量(註)
速度 \( \longleftrightarrow \) 温度
- 翻って,一般につぎのように言うことができる:
「物質量は多様に考えられるが,そこには次元の相似がある。」
| 註: |
熱量を「熱エネルギー」と同義と述べるテクストに出遭うことがあるが,これは間違い。
二つの概念が違うことは,「保存則」を挙げればよい。
熱量の概念は「保存則」を含蓄するが,「熱エネルギー」は保存則が立たない。
そして,そもそも物理学は,「熱エネルギー」を正式には定立していない。
熱量と「熱エネルギー」が同義だとする誤解は,何に由来するのか。
おそらく,両者の単位がともに J (ジュール) であることに由来する。
|
|
