流れが連続であるということを,式にする。
「連続」の表現は, 「質量保存」。
流管
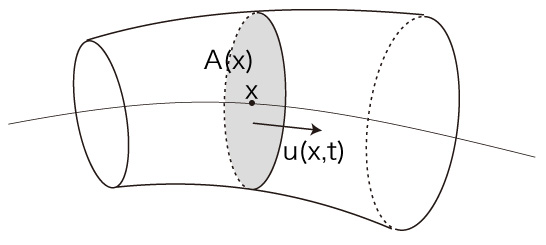
「流体の流れ」に対する質量保存則の適用は,3つの関数
| |
\( A(x) \) : x での流管の断面席
\( \rho(x, t) \) : (x, t) での流体の密度
\( u(x, t) \) : (x, t) での流速
|
のつぎの関係式を導く:
| |
\[A(x) \frac{\partial \rho(x, t)}{\partial t} \ + \ \frac{ \partial ( \rho(x,t) A(x) u(x,t) ) }{ \partial x } \frac{\ \ \ }{\ \ \ } \ = \ 0
\] |
|
この関係式を,「連続の式」と謂う。
「連続の式」導出の考え方は,「微小体積 \( A(x) \cdot \Delta x\) での流体の圧縮を表現する」。
以下,「連続の式」の導出:
(1) 時間tにおける,微小体積 \( A(x) \cdot \Delta x\) の質量の増加
\[
\rho(x, t+\Delta t) A(x) \Delta x - \rho(x, t) A(x) \Delta x
\]
(2) 時間tにおける,断面 \(A(x)\) へ時間 \(\Delta t\) に流入する流体の質量
\[
\rho(x,t) A(x) ( u(x,t) \Delta t )
\]
(3) 時間tにおける,断面 \(A(x + \Delta x)\) から時間 \(\Delta t\) に流出する流体の質量
\[
\rho(x+\Delta x,t) A(x+\Delta x) (u(x+\Delta x,t) \Delta t )
\]
質量保存則を適用すると,(1) = (2) - (3) より
\[
\rho(x, t+\Delta t) A(x) \Delta x - \rho(x, t) A(x) \Delta x \\
= \rho(x,t) A(x) u(x,t) \Delta t - \rho(x+\Delta x,t) A(x+\Delta x) u(x+\Delta x,t) \Delta t \\
\]
両辺を \( \Delta x\ \Delta t \) で割って,
\[
A(x) \frac{\rho(x, t+\Delta t) - \rho(x, t)}{\Delta t} \frac{\ \ \ \ }{\ \ \ \ } \\
\ \\
= - \ \frac{ \rho(x+\Delta x,t) A(x+\Delta x) u(x+\Delta x,t) - \rho(x,t) A(x) u(x,t) }{ \Delta x } \frac{\ \ \ \ \ \ \ \ \ \ \ }{\ \ \ \ \ \ \ \ \ \ \ }
\]
\( \Delta x \rightarrow 0, \ \Delta t \rightarrow 0 \) で,
\[
A(x) \frac{\partial \rho(x, t)}{\partial t} \
= - \ \frac{ \partial ( \rho(x,t) A(x) u(x,t) ) }{ \partial x } \frac{\ \ \ }{\ \ \ }
\]
移項して,
\[
A(x) \frac{\partial \rho(x, t)}{\partial t} \ + \ \frac{ \partial ( \rho(x,t) A(x) u(x,t) ) } { \partial x } \frac{\ \ \ }{\ \ \ } \ = \ 0
\]
| 註: |
連続の式は,他の方程式と組み合わせて使うことになるものであり,これ一つに用途を求めるというものではない。
|
|
