考え方は,「流体粒子の運動方程式」。 設定:
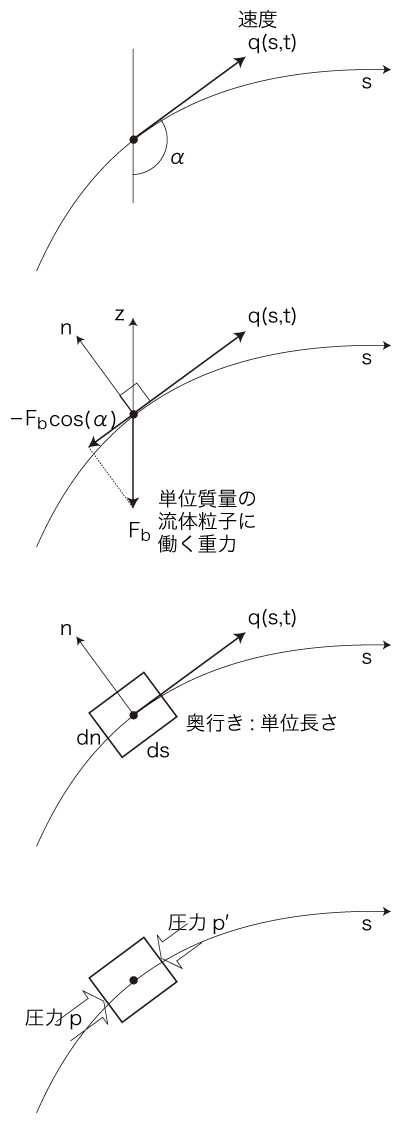
流体粒子の質量は,
流れの加速度は,
圧力 p′ は,
よって,流体粒子が受ける圧力は,
流体粒子に働く<流れ方向の力>は,
= 重力の流れ方向分力 (単位質量あたり) + 圧力 (単位質量あたり) ここで,

よって,
|
| Up | オイラーの運動方程式 | 作成: 2023-01-13 更新: 2023-01-13 |
考え方は,「流体粒子の運動方程式」。 設定:

流体粒子の質量は,
流れの加速度は,
圧力 p′ は,
よって,流体粒子が受ける圧力は,
流体粒子に働く<流れ方向の力>は,
= 重力の流れ方向分力 (単位質量あたり) + 圧力 (単位質量あたり) ここで,

よって,
|