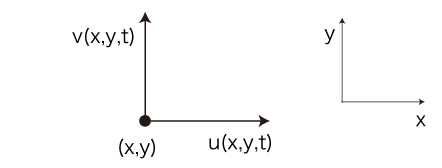流れが連続であるということを,式にする。
「連続」の表現は, 「質量保存」。
流体の中に平面を設定し,その上に \( (x y \) 直交座標をとる。
平面上の位置 \( ( x, y ) \),時間 \( t \) における \( x \) 軸方向と \( y \) 軸方向の速度を,それぞれ \( u( x, y, t ), v( x, y, t ) \) とする。
また,密度を \( \rho( x, y, t ) \) とする。
つぎの直方体の微小領域を考える:
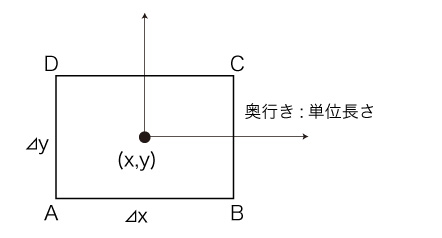
この領域に流入する質量と流出する質量は,同じでなければならない。
このことを,式で表す。
面 \( AD, BC \) での流体の速度の \( x \) 方向成分をそれぞれ \( u_{AB},\ u_{BC} \) で表し,面 \( AB, DC \) での流体の速度の \( y \) 方向成分をそれぞれ \( v_{AB},\ v_{DC} \) で表すとき,
\[
u_{AD} = u + \frac{ \partial u }{ \partial x }\ \Bigl( - \frac{ \Delta x }{ 2 }\ \Bigr) \\
\ \\
u_{BC} = u + \frac{ \partial u }{ \partial x }\ \frac{ \Delta x }{ 2 } \\
\ \\
v_{AB} = v + \frac{ \partial v }{ \partial y }\ \Bigl( - \frac{ \Delta y }{ 2 }\ \Bigr) \\
\ \\
v_{DC} = v + \frac{ \partial v }{ \partial y }\ \frac{ \Delta y }{ 2 } \\
\]
また,面 \( AD, BC, AB, DC \) での流体の密度をそれぞれ \( \rho_{AB},\ \rho_{BC},\ \rho_{AB},\ \rho_{DC} \) で表すとき,
\[
\rho_{AD} = \rho + \frac{ \partial \rho }{ \partial x }\ \Bigl( - \frac{ \Delta x }{ 2 }\ \Bigr) \\
\ \\
\rho_{BC} = \rho + \frac{ \partial \rho }{ \partial x }\ \frac{ \Delta x }{ 2 } \\
\ \\
\rho_{AB} = \rho + \frac{ \partial \rho }{ \partial y }\ \Bigl( - \frac{ \Delta y }{ 2 }\ \Bigr) \\
\ \\
\rho_{DC} = \rho + \frac{ \partial \rho }{ \partial y }\ \frac{ \Delta y }{ 2 } \\
\]
そして,\( AD, BC, AB, DC \) で単位時間に出入りする流体質量をそれぞれ \( m_{AD},\ m_{BC},\ m_{AB},\ m_{DC} \) で表すとき,
\[
\begin{align}
m_{AD} &= \rho_{AD}\ ( u_{AD}\ \Delta y ) \\
&= \Bigl(\ \rho + \frac{ \partial \rho }{ \partial x }\ \Bigl( - \frac{ \Delta x }{ 2 }\ \Bigr)\ \Bigr)
\Bigl(\ u + \frac{ \partial u }{ \partial x }\ \Bigl( - \frac{ \Delta x }{ 2 }\ \Bigr)\ \Bigr)\ \Delta y \\
&\approx
\Bigl(\ \rho\ u - \frac{ \Delta x }{ 2 }\
\Bigl(\ u\ \frac{ \partial \rho }{ \partial x }\ + \rho\ \frac{ \partial u }{ \partial x }\ \Bigr)\ \Bigr)\
\Delta y \\
\ \\
m_{AB} &= \rho_{AB}\ ( v_{AB}\ \Delta x ) \\
&= \Bigl(\ \rho + \frac{ \partial \rho }{ \partial y }\ \Bigl( - \frac{ \Delta y }{ 2 }\ \Bigr)\ \Bigr)
\Bigl(\ v + \frac{ \partial v }{ \partial y }\ \Bigl( - \frac{ \Delta y }{ 2 }\ \Bigr)\ \Bigr)\ \Delta x \\
&\approx
\Bigl(\ \rho\ v_ - \frac{ \Delta y }{ 2 }\
\Bigl(\ v\ \frac{ \partial \rho }{ \partial y }\ + \rho\ \frac{ \partial v}{ \partial y }\ \Bigr)\ \Bigr)\
\Delta x \\
\ \\
m_{BC} &= \rho_{BC}\ ( u_{BC}\ \Delta y ) \\
&= \Bigl(\ \rho + \frac{ \partial \rho }{ \partial x }\ \frac{ \Delta x }{ 2 }\ \Bigr)
\Bigl(\ u + \frac{ \partial u }{ \partial x }\ \frac{ \Delta x }{ 2 }\ \Bigr)\ \Delta y \\
&\approx
\Bigl(\ \rho\ u + \frac{ \Delta x }{ 2 }\
\Bigl(\ u\ \frac{ \partial \rho }{ \partial x }\ + \rho\ \frac{ \partial u }{ \partial x }\ \Bigr)\ \Bigr)\
\Delta y \\
\ \\
m_{DC} &= \rho_{DC}\ ( v_{DC}\ \Delta x ) \\
&= \Bigl(\ \rho + \frac{ \partial \rho }{ \partial y }\ \frac{ \Delta y }{ 2 }\ \Bigr)
\Bigl(\ v + \frac{ \partial v }{ \partial y }\ \frac{ \Delta y }{ 2 }\ \Bigr)\ \Delta x \\
&\approx
\Bigl(\ \rho\ v + \frac{ \Delta y }{ 2 }\
\Bigl(\ v\ \frac{ \partial \rho }{ \partial y }\ + \rho\ \frac{ \partial v }{ \partial y }\ \Bigr)\ \Bigr)\
\Delta x \\
\end{align}
\]
微小領域の単位時間あたりの質量増減量は,
\[
\frac{ \partial \rho }{ \partial y }\ ( \Delta x \Delta y ) \\
= m_{AD} + m_{AB} - m_{BC} - m_{DC} \\
\ \\
= \Bigl(\ \rho\ u - \frac{ \Delta x }{ 2 }\
\Bigl(\ u\ \frac{ \partial \rho }{ \partial x }\ + \rho\ \frac{ \partial u }{ \partial x }\ \Bigr)\ \Bigr)\
\Delta y \\
+ \Bigl(\ \rho\ v_ - \frac{ \Delta y }{ 2 }\
\Bigl(\ v_\ \frac{ \partial \rho }{ \partial y }\ + \rho\ \frac{ \partial v}{ \partial y }\ \Bigr)\ \Bigr)\
\Delta x \\
- \Bigl(\ \rho\ u + \frac{ \Delta x }{ 2 }\
\Bigl(\ u\ \frac{ \partial \rho }{ \partial x }\ + \rho\ \frac{ \partial u }{ \partial x }\ \Bigr)\ \Bigr)\
\Delta y \\
- \Bigl(\ \rho\ v + \frac{ \Delta y }{ 2 }\
\Bigl(\ v\ \frac{ \partial \rho }{ \partial y }\ + \rho\ \frac{ \partial v }{ \partial y }\ \Bigr)\ \Bigr)\
\Delta x \\
\ \\
= - \Bigl(\ u\ \frac{ \partial \rho }{ \partial x }\ + \rho\ \frac{ \partial u }{ \partial x }\ \Bigr)\ \Delta x \Delta y\
- \Bigl(\ v_\ \frac{ \partial \rho }{ \partial y }\ + \rho\ \frac{ \partial v}{ \partial y }\ \Bigr)\ \Delta x \Delta y \\
\]
よって,
\[
\frac{ \partial \rho }{ \partial t }
= - u\ \frac{ \partial \rho }{ \partial x }\
- \rho\ \frac{ \partial u }{ \partial x }
- v\ \frac{ \partial \rho }{ \partial y }\
- \rho\ \frac{ \partial v}{ \partial y }\\
\]
\( \rho \) の実質微分が
\[
\frac{ D \rho }{ D t } = \frac{ \partial \rho }{ \partial t } + \Big(\ u\ \frac{ \partial \rho }{ \partial x } + v\ \frac{ \partial \rho }{ \partial y }\ \Bigr)
\]
なので,
\[
\frac{ D \rho }{ D t }
= \frac{ \partial \rho }{ \partial t }
- \Big(\ \frac{ \partial \rho }{ \partial t } + \rho\ \frac{ \partial u }{ \partial x } + \rho\ \frac{ \partial v }{ \partial y }\ \Bigr) \\
\]
結局,
\[
\frac{ D \rho }{ D t }
= - \rho\ \Bigl(\ \frac{ \partial u }{ \partial x } +\ \frac{ \partial v }{ \partial y }\ \Bigr) \\
\]
これを,「連続の式」と謂う。
|