2次元流れの運動方程式を求める。
考え方は,「\( x \) 方向に流体粒子にかかる力」。
設定:
- 流体の密度:\( \rho \)
- 流体粒子と流速:
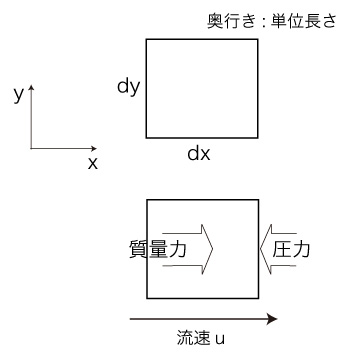
流体において,単位質量に \( x \) 方向に働く力を, \( X \) とする。
このとき,上の粒子には,\( x \) 方向につぎの力がかかる:
\[
X \times ( \rho \times ( dx \times dy \times 1 ) ) = \rho\ dx\ dy\ X
\]
粒子には,この力と反対方向に,圧力 \( p( x ) \) による力がかかる:
\[
x 方向に粒子に働く<単位長さあたりの単位面積あたりの力> = - \frac{ dp }{ dx } \\
\Longrightarrow \ \ x 方向に粒子に働く<単位面積あたり力> = \Bigl( - \frac{ dp }{ dx }\ \Bigr)\ dx \\
\Longrightarrow \ \ x 方向に粒子に働く力: \Bigl( - \frac{ dp }{ dx }\ dx \Bigr)\ \times ( dy \times 1 )
= - \frac{ dp }{ dx }\ dx\ dy \\
\]
よって,粒子に \( x \) 方向にかかる力は,
\[
\rho\ dx\ dy\ X - \frac{ dp }{ dx }\ dx\ dy \\
\]
一方,粒子に \( x \) 方向にかかる力は, \( x \) 方向の流速 \( u \) を用いてつぎのように表現される:
\[
質量 \times 加速度 = ( \rho\ dx\ dy ) \times \frac{ Du }{ Dt }
\]
以上まとめて,
\[
\rho\ dx\ dy\ X - \frac{ dp }{ dx }\ dx\ dy
= \rho\ dx\ dy\ \frac{ Du }{ Dt }
\]
両辺を \( \rho\ dx\ dy \) で割って,
\[
X - \frac{ 1 }{ \rho }\frac{ dp }{ dx }
= \frac{ Du }{ Dt }
\]
ここで,
\[
\frac{ D u }{ D t }
= \frac{ \partial u }{ \partial t }
+ u\ \frac{ \partial u }{ \partial x }
+ v\ \frac{ \partial u }{ \partial y }
\]
なので,結局,
\[
X - \frac{ 1 }{ \rho }\frac{ dp }{ dx }
= \frac{ \partial u }{ \partial t }
+ u\ \frac{ \partial u }{ \partial x }
+ v\ \frac{ \partial u }{ \partial y }
\]
この式を,2次元流れのオイラーの運動方程式という。
|
