面Aが,流速 U の流体から力を受ける:

dA を,Aの微小領域とする。
dA が受ける力を,「圧力」\( p \) と「壁面剪断力」\( \tau_w \) の合成に見なす── \( p \) と \( \tau_w \) の方向はつぎのようにとる:

\( p \) と \( \tau_w \) を,流れ方向とこれに垂直な方向を用いて,<分力の合成>に表す:

「抗力 (drag)」\( D \) を<流れ方向に作用する力>として,「揚力 (lift)」\( L \) を<流れの垂直方向に作用する力>として,それぞれつぎのように定義する:
\[
D = D_p + D_f \\
L = - (L_p + L_f )
\]
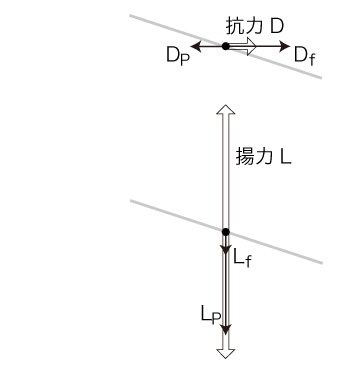
また,\( D_p, D_f, L_p, L_f \) を,つぎのように呼ぶ:
\( D_p \) :「圧力抗力 (pressure drag)」
\( D_f \) :「摩擦抗力 (friction drag)」
\( L_p \) :「圧力揚力 (pressure lift)」
\( L_f \) :「擦揚揚力 (friction lift)」
そして「流体力 (flow force)」\( F\) を,抗力 \( D \) と揚力 \( L \) の合成として定義する:
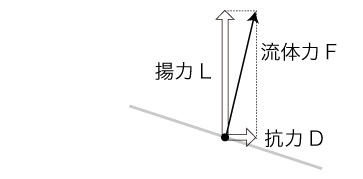
流体に対する面の傾きを,つぎのように表す:

このとき,
\[
D = D_p + D_f = ( - p\ cos( \theta ) ) + \tau_w\ sin( \theta ) \\
L = - (L_p + L_f ) = - ( p\ sin( \theta ) ) + \tau_w\ cos( \theta ) ) \\
\]
\( F, D, L, D_p, D_f, L_p, L_f \) は,\( dA \) に対して定まる。
このことを示すために,改めてつぎのように書く:
\( (F)_{dA}, (D)_{dA}, (L)_{dA}, (D_p)_{dA}, (D_f)_{dA}, (L_p)_{dA}, (L_f)_{dA} \)
このとき,つぎが面積Aの抗力・揚力・流体力の式になる:
\[
F_A = D_A + L_A \\
\ \\
D_A = ( D_p )_A + ( D_f )_A \\
( D_p )_A = \int_A^{} (D_p)_{dA}\ dA \\
( D_f )_A = \int_A^{} (D_f)_{dA}\ dA \\
\ \\
L_A = ( L_p )_A + ( L_f )_A \\
( L_p )_A = \int_A^{} (L_p)_{dA}\ dA \\
( L_f )_A = \int_A^{} (L_f)_{dA}\ dA \\
\]
定義は,定義に過ぎない。
抗力・揚力を定義した積分式は,実際に扱えるものではない。
抗力・揚力は,概算式をつくりそれで計算している。
|





