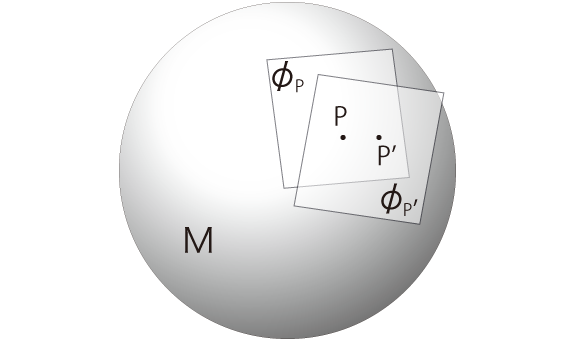
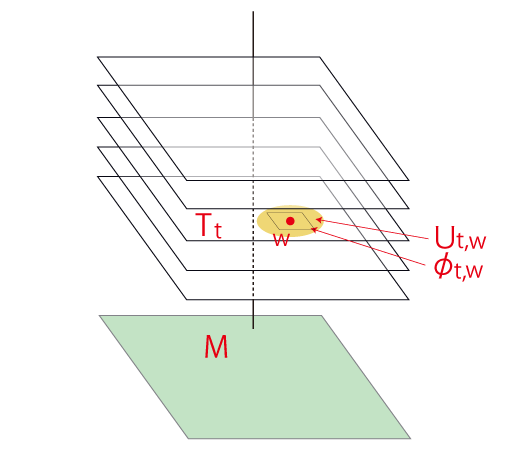
上は,球面をモデルにした,「球面に沿って,接平面をシフト」の絵。 下は,「接平面を束ねる軸に沿って,接平面をシフト」の絵。 多様体を前者の絵で描くときこれを「面多様体」と呼び,後者の絵で描くときこれを「「束多様体」と呼ぶことにする。 接平面を「実際 practical 空間」とし,束ねる軸を「時間軸」としてとると,この「束多様体」論は『相対性理論』になる。 時間軸をとることの意味は,空間を「運動する空間」にすることである。 「接平面をシフト」は,「実際 practical 空間の進化」の意味になる。 
『特殊相対性理論』は,運動を「等速運動」に設定した場合である。 このとき「実際空間の進化」は,向きを保つが,長さが変わる。 『一般相対性理論』は,運動を「慣性運動」へと一般化した場合である。 このとき「実際空間の進化」は,向きも変わる。 向きを変えるものは,「重力」という空間構造である。 「面多様体」は,これの形がわかっているものとして立つ。 一方,「束多様体」は,これの形がわからないものとして立つ。 即ち,<実空間>がわからないものとして立つ。 ここで「わからないものとして立つ」の意味は,「もとより,外形が演繹されてくる論理体系ではない」である。 われわれは,宇宙の形を知ることができない。 この「できない」の数学的意味は,「束多様体は外形が演繹されてくる論理体系ではない」である。 |