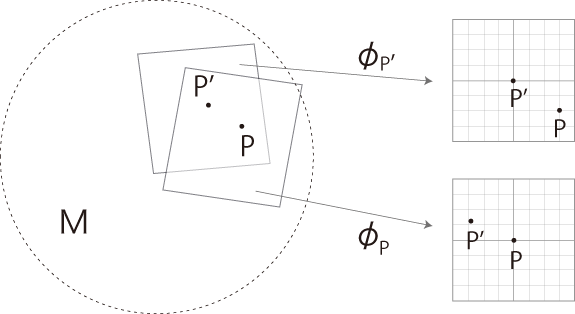
地図 \( \phi_{P}\) は,\( P \) における \( M\) の接平面に,固定されて乗っている。 この「固定」には,つぎのことが含まれる:
この面に,\( P \) から観察される世界を写す。 写し方は,投影法である: 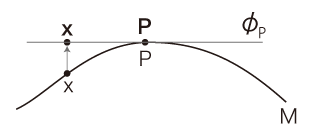
地図の座標は,すべての地図で同じ規格である。 デカルト座標の基底ベクトルを,
|
| Up | デカルト座標 | 作成: 2018-02-13 更新: 2018-02-15 |
地図 \( \phi_{P}\) は,\( P \) における \( M\) の接平面に,固定されて乗っている。 この「固定」には,つぎのことが含まれる:

この面に,\( P \) から観察される世界を写す。 写し方は,投影法である: 
地図の座標は,すべての地図で同じ規格である。 デカルト座標の基底ベクトルを,
|