わたしの<いま・ここ>を知るとは,わたしが<いま・ここ>に至った経緯を知ることである。 そこで,わたしの過去を調べるとする。 わたしの過去は,これまでのわたしの<いま・ここ>の地図に記されている。 <いま・ここ>は時空間の点 \( (t, w)\) であり,その地図は \(\phi_{t,w}\) である。 そこで,過去の記録の検索は, \(\phi_{t',w}\, (t'< t)\) を溯るというやり方になる。 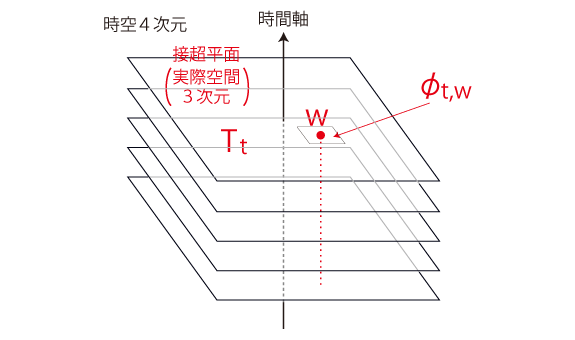
よって, わたしの<いま・ここ> \( (t’, w)\) の \(w\) は,固定される。 「一般相対性」とは,《わたしに対し周りが動く》ということである。 地図溯行の作業は,<地図を接ぐ>である。 わたしの<いま・ここ>の地図 \(\phi_{t',w}\, ( t' < t ) \) を順番に接いでいく。 地図 \(\phi_{t_1,w}\) に地図 \(\phi_{t_2,w}\) を接ぐとは,\(\phi_{t_2,w}\) に \(\phi_{t_1,w}\) を読み込むということである。 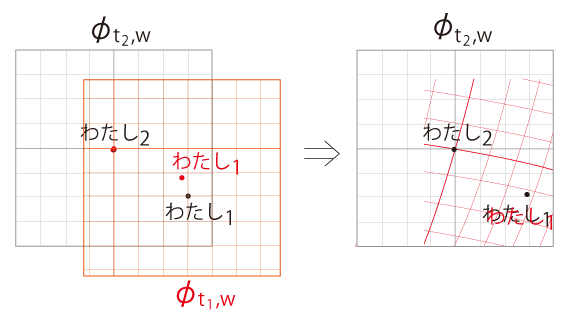
こうして得られる<いま・ここ>の系列は,ミンコフスキー空間の \(t\,xyz\) 座標に記すのが便利である。 即ち,一つの<いま・ここ>を原点に定め,これと相対的に他の<いま・ここ>をプロットする。 ただしこの座標は4次元である。 \(y,\,z\) 座標を使わなくて済む場面設定が都合よくできれば,つぎの \(t\,x\) 座標──即ち,\(t\) 軸と\(x\) 軸が張る座標面──で足りることになる。 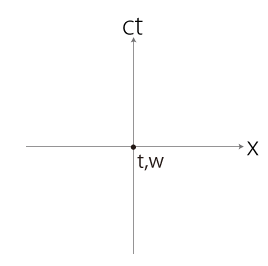
ともかく,以上の作業の結果,わたしの軌跡がミンコフスキー空間の<世界線>の一つとして描かれることになる。 例えばつぎのように描かれたとする: 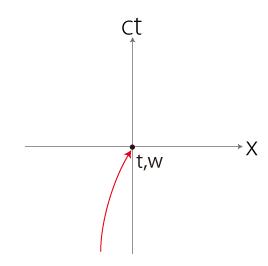
以上が,「地図」の用法である。 |