位置: \( ( ct, {\bf x} ) \) 速度: \( \bf u \) これにかかっている力:\( \bf F \) 
このとき, 「仕事」のイメージは \( {\bf f} \cdot d{\bf x} \) であり,したがって \[ {\bf f} \cdot \frac{d{\bf x}}{dt} = {\bf f} \cdot {\bf v} \] が「仕事率」ということになる。 そして仕事率 \( {\bf f} \cdot {\bf v} \) に対しては,つぎが仕事の式になる: \[ \int {\bf f} \cdot {\bf v}\, dt \] これを, 「仕事の4元化」の目論見を以て,計算してみる: 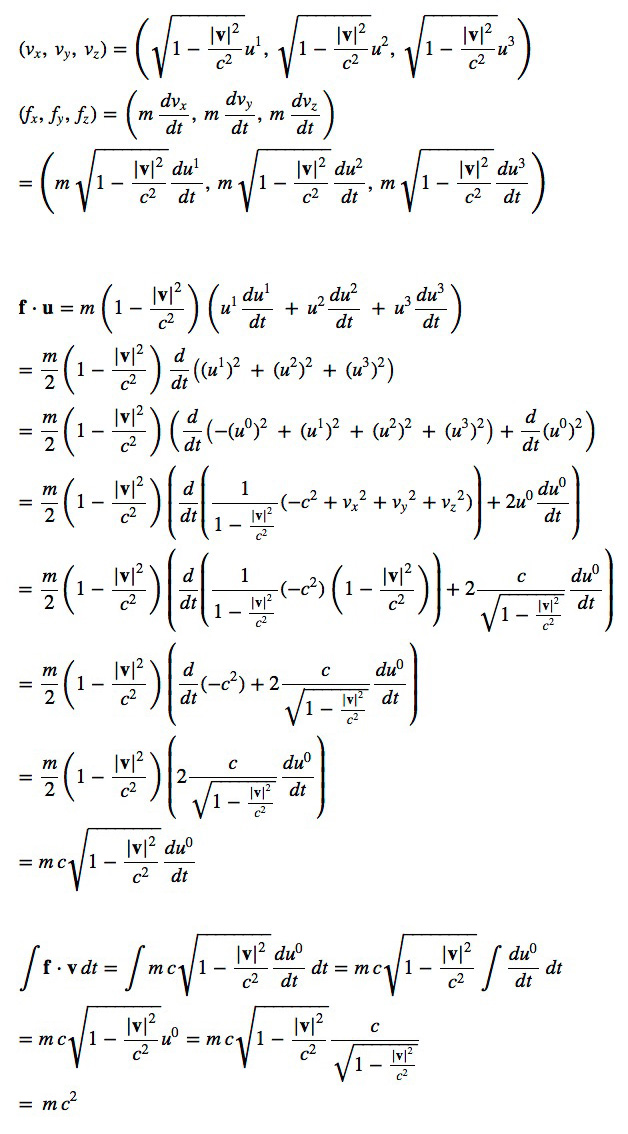
結局,「仕事 \( \int {\bf f} \cdot {\bf v}\, dt \) 」が,慣性系に依らない値で得られた。 そこでこれを,エネルギーの4元化と定める:
|