つぎの問題を考える:
観測者Sと,Sに対し相対速度Vで等速運動する観測者Tがいる。
Sにおける長さ \( L_S \) は,Tにおいては長さ \( L_T \) になるとする。
\( L_S \) に対する \( L_T \) の比率rは?
与条件:光の速度は,これを観測する者に依らず一定cである。
|
生活感覚は, 「速度は相対的,長さは絶対」である。
「光速は絶対」ということにすると「長さは相対的」になるというのが,この問いの趣旨である。
比率rを求める手法は,思考実験である。
自分を観察者Aにして,長さ \( L = L_S \) を速度Vで等速運動させる。
そして,このときのこれの長さ \( L_1 \) を計算する。
この \( L_1 \) をつぎのように考える:
Sで静止している \( L_S \) は,Tでは比率rを以て長さ \( L_T \) になる。
Tで静止している \( L_T \) は,Sでは比率rを以て長さ \( L_1 \) になる。
ここでは,つぎの二つを等しくrであるとしている:
Tの静止長さに対する,Sがこれに観る長さの比率
Sの静止長さに対する,Tこれに観る長さの比率
このように設定するのは,SとTの立場は相対的と見ることになるからである:
こうして,\( L \) に対する \( L_1 \) の比率Rは,rとrの合成 \( r^2 \) ということになる。
したがって,つぎのようになる:
以下,rを求める。
線分 \( AB \) の長さが \( L \) であるとする。
この線分の中点をMとする。
tx座標を導入し,A, M, B の世界線 \( w_A ,\, w_M ,\, w_B \) を書く。
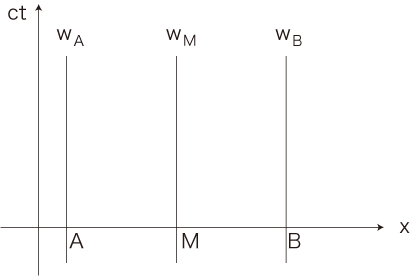
つぎに,この線分が,線分 \( A^{'}B^{'} \) (中点 \( M^{'} \) ) としてx軸方向に速度Vで等速運動する様を考える。
これの世界線 \( w_{A^{'}} ,\, w_{M^{'}} ,\, w_{B^{'}} \) を書く。
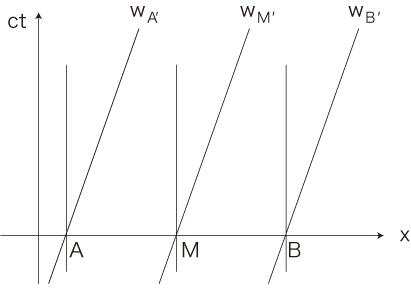
つぎに,ct = 0 で \( M \) より光が発せられた,と考える。
光は,この図では \( A^{'} \rightarrow ( A と B ) \rightarrow B^{'} \) の順に到達する:
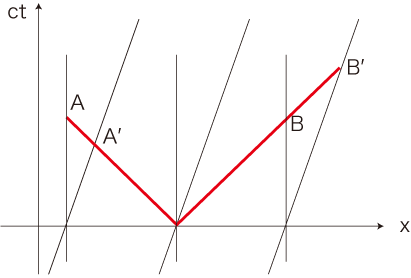
それぞれの到達時間を,\( ct_{A^{'}}, ct_0, ct_{B^{'}} \) とする。
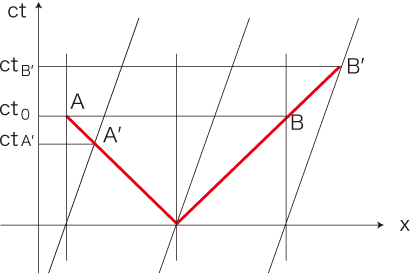
これより:
\[
AB = AM + MB = ct_0 + ct_0 = 2\, ct_0 \\
A^{'}B^{'} = M^{'}A^{'} + M^{'}B^{'} = (ct_0 - Vt_{A^{'}}) + (ct_0 + Vt_{B^{'}}) = 2\, ct_0 + V (t_{B^{'}} - t_{A^{'}} ) \\
\]
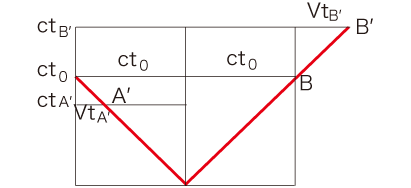
また,図中の光の軌跡を表す線は,傾きが 1 になっているから,
\[
Vt_{A^{'}} = ct_0 - ct_{A^{'}} \Longrightarrow ( c + V) t_{A^{'}} = c t_0 \Longrightarrow t_{A^{'}} = \frac{c t_0}{c + V } \\
Vt_{B^{'}} = ct_{B^{'}} - ct_0 \Longrightarrow (c - V) t_{B^{'}} = c t_0 \Longrightarrow t_{B^{'}} = \frac{c t_0}{c - V} \\
t_{B^{'}} - t_{A^{'}} = \frac{c t_0}{c - V} - \frac{c t_0}{c + V }
= \frac{2\,V\,c t_0}{c^2 - V^2 }
\]
よって
\[
A^{'}B^{'} = 2\, ct_0 + V (t_{B^{'}} - t_{A^{'}} )
= 2\, ct_0 + \frac{2\,V^2\,c t_0}{c^2 - V^2 }
= \frac{2\,c t_0\, c^2}{c^2 - V^2 } \\
R = \frac{A^{'}B^{'}}{AB} = \frac{c^2}{c^2 - V^2 } = \frac{1}{1 - \frac{V^2}{c^2} } \\
r = \frac{1}{\sqrt{1 - \frac{V^2}{c^2} }}
\]
|




