「ローレンツ収縮」で,つぎの図を導いた: 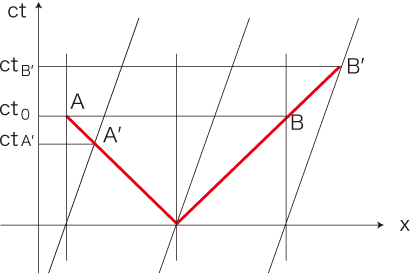
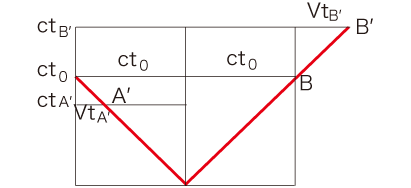
これに対し,つぎの時間を読む:
\( T,\,T_1 \) は,つぎのようになる:
これをつぎのように読む:
「時間がゆっくり進む」 「時間が収縮する」 そして「長さの収縮」のときのように,
Sの時間は,Tでは比率rを以て収縮する。 Tの時間は,Sでは比率rを以て収縮する。
|
| Up | 「時間がゆっくり進む」 | 作成: 2017-12-03 更新: 2017-12-03 |
「ローレンツ収縮」で,つぎの図を導いた: 

これに対し,つぎの時間を読む:
\( T,\,T_1 \) は,つぎのようになる:
これをつぎのように読む:
「時間がゆっくり進む」 「時間が収縮する」 そして「長さの収縮」のときのように,
Sの時間は,Tでは比率rを以て収縮する。 Tの時間は,Sでは比率rを以て収縮する。
|