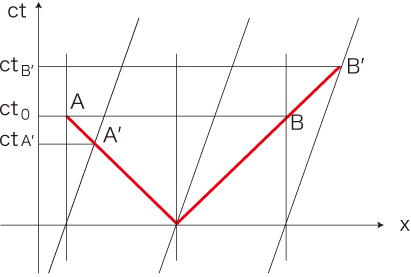
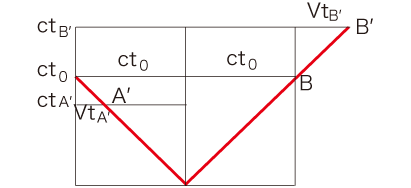
これを,「\( A \rightarrow A^{'},\, B \rightarrow B^{'} \) を導く座標変換」と読むことにする:
「\( A^{'} \) と \( B^{'} \) は同時」を示す線 \( A^{'}B^{'} \) を引く:
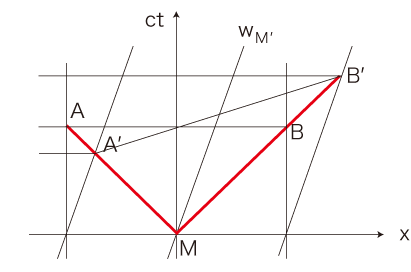
世界線 \( w_{M^{'}} \) と \( A^{'}B^{'} \) をもとにして,座標枠をつくる:
Bの座標 \( ( c\,t_0, c\,t_0 ) \) に対し,\( B^{'} \) の \( tx \) 座標は \( \left( c\,t_0 + V \frac{c t_0}{c - V}, c\,t_0 + V \frac{c\,t_0}{c - V} \right) \)
( 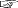 「ローレンツ収縮」) )。 「ローレンツ収縮」) )。
そして,
\[
c\,t_0 + V \frac{c\,t_0}{c - V} = c\,t_0 \left( 1 + V \frac{1}{c - V} \right) = c\,t_0 \frac{c}{c - V}
\]
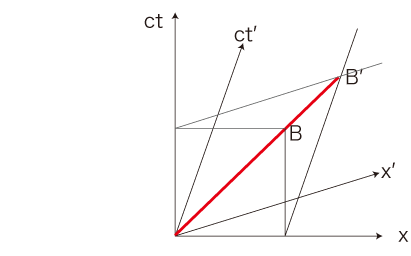
よって,つぎの図が導かれる:
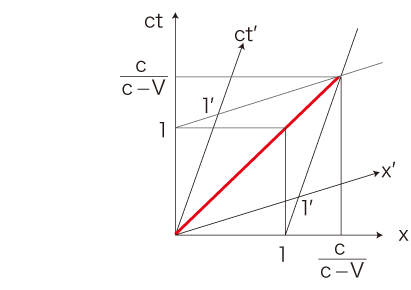
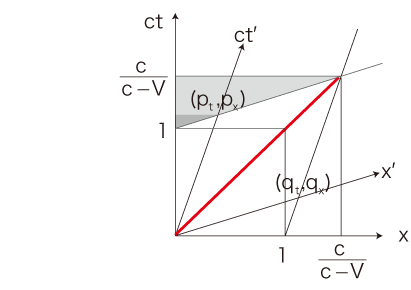
\( c^{'}t^{'} \) 座標 \( (1^{'},\, 0),\, (0,\, 1^{'}) \) の \( ct \) 座標 \( ( p_t, p_x ),\, ( q_t, q_x ) \) は:
\[
\frac{p_t}{p_x} = ( ct^{'} 軸の傾き ) = \frac{c}{V} \\
\frac{p_t - 1}{p_x} = ( x^{'} 軸の傾き ) = \frac{V}{c}\\
\]
これより,
\[
( p_t, p_x ) = \left( \frac{c^2}{c^2 - V^2} ,\, \frac{cV}{c^2 - V^2} \right)
= \left( \frac{1}{1 - \frac{V^2}{c^2}} ,\, \frac{ \frac{V}{c}}{1 - \frac{V^2}{c^2}} \right) \\
( q_t, q_x ) = ( 対角線に対し ( p_t, p_x ) と対称)
= \left( \frac{ \frac{V}{c}}{1 - \frac{V^2}{c^2}} ,\, \frac{1}{1 - \frac{V^2}{c^2}} \right)
\]
\( \frac{ 1}{1 - \frac{V^2}{c^2}} \) はローレンツ収縮の比率 \( \frac{1}{\sqrt{1 - \frac{V^2}{c^2}}} \) の2乗と見るべきものなので,\( t^{'}x{'} \) 座標の (1, 0), (0, 1) を,\( tx \) 座標のつぎの点に定める:
\[
\left( \frac{1}{\sqrt{1 - \frac{V^2}{c^2}}} ,\, \frac{\frac{V}{c}}{\sqrt{1 - \frac{V^2}{c^2}}} \right) ,\ \
\left( \frac{ \frac{V}{c}}{\sqrt{1 - \frac{V^2}{c^2}}} ,\, \frac{1}{\sqrt{1 - \frac{V^2}{c^2}}} \right)
\]
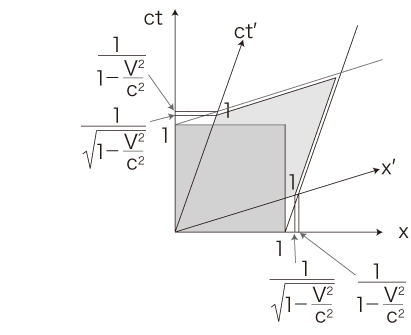
ここで,つぎのように措く:
\[
\gamma = \frac{1}{\sqrt{1 - \frac{V^2}{c^2}}} ,\ \
\beta = \frac{V}{c}
\]
このとき,座標変換がつぎの式になる:
\[
\left(
\begin{array}{c}
c\,t^{'} \\
x^{'} \\
\end{array}
\right)
=
\left(
\begin{array}{cc}
\gamma & - \gamma \beta \\
- \gamma \beta & \gamma \\
\end{array}
\right)
\left(
\begin{array}{c}
c\,t \\
x \\
\end{array}
\right) \\
=
\gamma
\left(
\begin{array}{cc}
1 & - \beta \\
- \beta & 1 \\
\end{array}
\right)
\left(
\begin{array}{c}
c\,t \\
x \\
\end{array}
\right)
=
\gamma
\left(
\begin{array}{ccc}
c\,t &- &\beta x \\
- \beta\, c\,t &+& x \\
\end{array}
\right)
\]
あるいは
\[
\left(
\begin{array}{c}
w^{'} \\
x^{'} \\
\end{array}
\right)
=
\gamma
\left(
\begin{array}{cc}
1 & - \beta \\
- \beta & 1 \\
\end{array}
\right)
\left(
\begin{array}{c}
w \\
x \\
\end{array}
\right)
=
\gamma
\left(
\begin{array}{ccc}
w &-& \beta x \\
- \beta\, w &+& x \\
\end{array}
\right)
\]
この変換を「(x方向の) ローレンツ変換」と呼ぶ。
翻って,ローレンツ収縮──「長さが縮まる」「時間がゆっくり進む」──は,この変換の含意として導かれるものになる。
|




 「ローレンツ収縮」) )。
「ローレンツ収縮」) )。


