Sの原点Oからx方向に速度vで移動する点に,t,x,y,z 座標系S' を立てる:
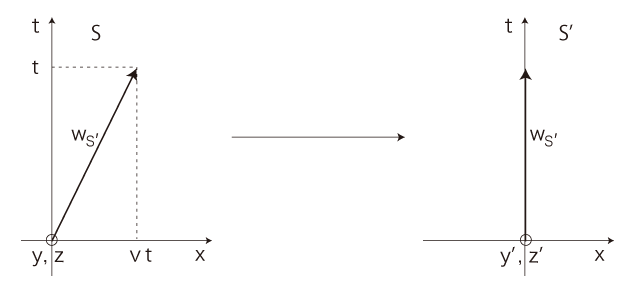
( \(W_{S'}\) は,S' の最初の原点の世界線)
仮定1. 線型性
| |
S における等速直線運動は,S' でも等速直線運動。
即ち,同一点のSにおける座標 ( t, x, y, z ) とS' における座標 ( t' , x', y', z' ) との間の変換は,線型変換。
|
|
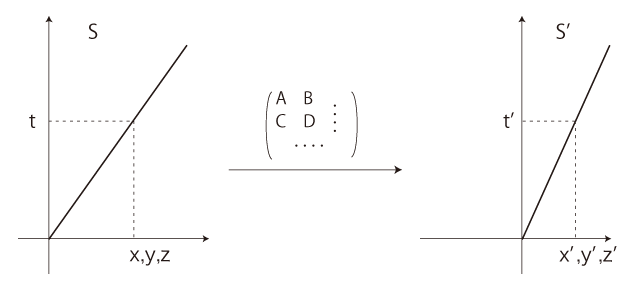
S, S' 間の \(W_{S'}\) (S' の最初の原点の世界線) の対応が,つぎのようであるとする:
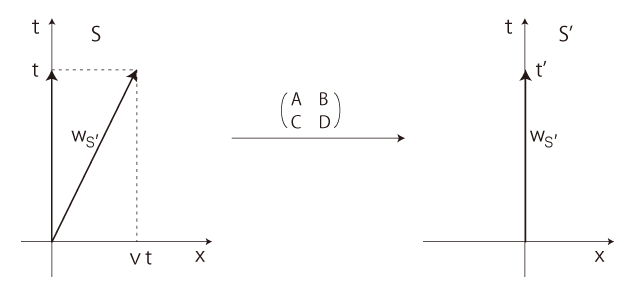
\[
\left(
\begin{array}{cc}
A & B \\
C & D \\
\end{array}
\right)
\left(
\begin{array}{c}
t \\
vt \\
\end{array}
\right)
=
\left(
\begin{array}{c}
t' \\
0 \\
\end{array}
\right)
\\ \\
At + Bvt = t'
\Longrightarrow \ \frac{t'}{t} = A + Bv
\\
Ct + Dvt = 0 \
\Longrightarrow \ D = -\frac{C}{v}
\]
S' 系に対し,S 系は x方向に速度 \(-v\) で移動している。
S, S' 間の \(W_S\) (S の最初の原点の世界線) の対応が,つぎのようであるとする:
( t, t’ は,上の t, t' とは別)
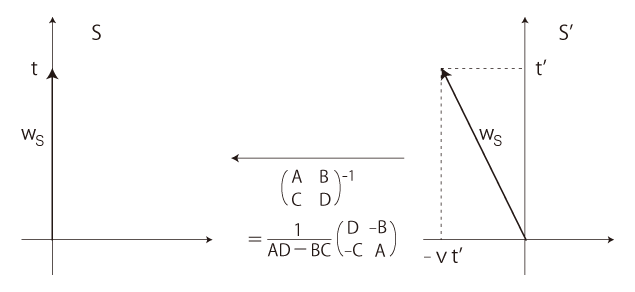
\[
\left(
\begin{array}{c}
t \\
0 \\
\end{array}
\right)
=
\frac{1}{AD-BC}
\left(
\begin{array}{cc}
D & -B \\
-C & A \\
\end{array}
\right)
\left(
\begin{array}{c}
t' \\
-vt' \\
\end{array}
\right)
\\ \\
t = \frac{1}{AD-BC} ( Dt' + Bvt' )
\Longrightarrow \ \frac{t'}{t} = \frac{AD-BC}{D + Bv}
\\
0 = \frac{1}{AD-BC} ( -Ct' - Avt' )
\Longrightarrow \ C = -Av
\]
\[
D = -\frac{C}{v},\ C = -Av \
\Longrightarrow \ D = A
\]
よって,
\[
\left(
\begin{array}{cc}
A & B \\
C & D \\
\end{array}
\right)
=
\left(
\begin{array}{cc}
A & B \\
-Av & A \\
\end{array}
\right)
\]
時間0で原点からx方向に発した光点の世界線が,S, S' 間でつぎのように対応しているとする:
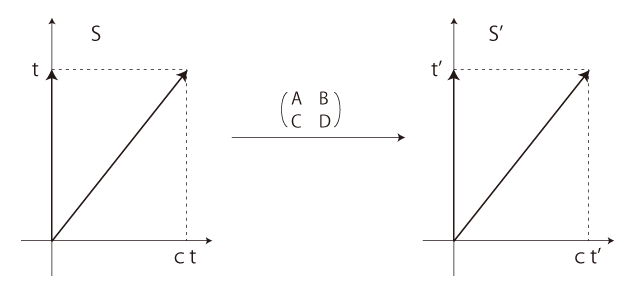
\[
\left(
\begin{array}{c}
t' \\
ct' \\
\end{array}
\right)
=
\left(
\begin{array}{cc}
A & B \\
C & D \\
\end{array}
\right)
\left(
\begin{array}{c}
t \\
ct \\
\end{array}
\right)
=
\left(
\begin{array}{cc}
A & B \\
-Av & A \\
\end{array}
\right)
\left(
\begin{array}{c}
t \\
ct \\
\end{array}
\right)
\\ \\
t' = At + Bct \
\Longrightarrow \ \frac{t'}{t} = A + Bc
\\
ct' = -Avt + Act \
\Longrightarrow \ \frac{t'}{t} = A \frac{c-v}{c} = A \left( 1 - \frac{v}{c} \right)
\\ \\
A + Bc = \frac{t'}{t} = A \frac{c-v}{c} \
\Longrightarrow \ B = \frac{1}{c} \left( A \frac{c-v}{c} - A \right) = - A \frac{v}{c^2}
\]
よって,
\[
\begin{align*}
\left(
\begin{array}{cc}
A & B \\
C & D \\
\end{array}
\right)
&=
\left(
\begin{array}{cc}
A & - A \frac{v}{c^2} \\
-Av & A \\
\end{array}
\right)
\\
&=
A
\left(
\begin{array}{cc}
1 & - \frac{v}{c^2} \\
-v & 1 \\
\end{array}
\right)
\end{align*}
\]
仮定3. ミンコフスキー計量
| |
\( -c^2t^2 + x^2 + y^2 + z^2 = -c^2t'^2 + x'^2 + y'^2 + z'^2 \)
|
|
\[
\begin{align*}
\left(
\begin{array}{c}
t' \\
x' \\
\end{array}
\right)
&=
\left(
\begin{array}{cc}
A & B \\
C & D \\
\end{array}
\right)
\left(
\begin{array}{c}
t \\
x \\
\end{array}
\right)
=
A
\left(
\begin{array}{cc}
1 & - \frac{v}{c^2} \\
-v & 1 \\
\end{array}
\right)
\left(
\begin{array}{c}
t \\
x \\
\end{array}
\right)
\\&=
A
\left(
\begin{array}{c}
t - \frac{v}{c^2} x\\
-vt + x \\
\end{array}
\right)
\end{align*}
\\ \\
-c^2t^2 + x^2 + y^2 + z^2
\\= -c^2t'^2 + x'^2 + y'^2 + z'^2
\\= -c^2 A^2 \left( t - \frac{v}{c^2} x \right) ^2 + A^2 (-vt + x)^2 + y^2 + z^2
\\= A^2 \left( -c^2t ^2 + 2v tx - \frac{v^2}{c^2}x^2 + v^2t ^2 -2vtx + x^2 \right) + y^2 + z^2
\\= A^2 \left( -c^2t ^2 + x^2 - \frac{v^2}{c^2} ( -c^2t ^2 + x^2 ) \right) + y^2 + z^2
\\= A^2 ( -c^2t ^2 + x^2 ) \left(1 - \frac{v^2}{c^2} \right) + y^2 + z^2
\\ \\
\quad \Longrightarrow -c^2t^2 + x^2 = A^2 ( -c^2t ^2 + x^2 ) \left(1 - \frac{v^2}{c^2} \right)
\\ \quad \Longrightarrow 1 = A^2 \left(1 - \frac{v^2}{c^2} \right)
\\ \quad \Longrightarrow A^2 = \frac{1}{1 - \frac{v^2}{c^2}}
\]
WS′ の対応,WS の対応,光点の世界線の対応のところで,それぞれ \( \frac{t'}{t} \) がつぎのように導かれた:
\[
\frac{t'}{t} = A + Bv
\\ \frac{t'}{t} = \frac{AD-BC}{D + Bv}
\\\frac{t'}{t} = A \left( 1 - \frac{v}{c} \right)
\]
これらは, B, C, D を A に対して表すことで,つぎのようになる:
\[
\frac{t'}{t} = A + \left( - A \frac{v}{c^2} \right) v = A \left( 1 - \frac{v^2}{c^2} \right)
\\ \frac{t'}{t} = \frac{AD-BC}{D + Bv}
= \frac{AA - \left( - A \frac{v}{c^2} \right) ( -Av )} {A + \left( - A \frac{v}{c^2} \right) v}
= \frac{ A \left( 1 - \frac{v^2}{c^2} \right) } {1 - \frac{v^2}{c^2} }
= A
\\\frac{t'}{t} = A \left( 1 - \frac{v}{c} \right)
\]
場合ごとに,\( \frac{t'}{t} \) の値が違ってくるわけである。
ただし,各関係は \( A > 0 \) を導くものになっている。
したがって,
\[
A = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}
\]
ここで,つぎのように措く:
\[
\beta_v = \frac{v}{c}
\\ \gamma_v = \frac{1}{\sqrt{1 - {\beta_v}^2}}
\]
このとき
\[
\begin{align*}
\left(
\begin{array}{cc}
A & B \\
C & D \\
\end{array}
\right)
&=
A
\left(
\begin{array}{cc}
1 & - \frac{v}{c^2} \\
-v & 1 \\
\end{array}
\right)
=
\gamma_v
\left(
\begin{array}{cc}
1 & - \frac{\beta_v}{c} \\
- \beta_v c & 1 \\
\end{array}
\right)
\end{align*}
\]
|